针对流密码的观察者攻击
参考资料
待选文献
以下所有文献均来自IACR,国际密码学论文的预发印期刊
- 针对RSA gcd的测信道缓存耗时攻击
- ECDSA侧信道攻击
- 针对基于伪随机词数组的流密码的区分攻击
- 针对原始RC4的差分攻击
只针对RC4,想看懂这个还需要从头学习RC4…… - 针对基于 LFSR (线性反馈移位寄存器) 的流密码的快速相关攻击 (FCA)的量子算法
只有理论,还无法实践 - 针对有限密钥周期的小状态流密码的多采样快速相关性攻击
看不太懂 - 针对流密码的观察者攻击 - MTNS2022入选论文
PDF只有八页,钻研个把天至少也能搓出板子
国际数学网络与系统理论研讨会接收的论文,含金量这块肯定没问题 - 印度理工学院 - 三步走流密码侧信道攻击
机器学习……吓哭了
参考资料
- 维基百科 - 流密码
- 维基百科 - GF域上的本原多项式
- AMD手册 - LSFR如何实现
- 维基百科 - 线性反馈移位寄存器
- 博客园 - 字节位序反转算法
- Github仓库 - 伯利坎普梅塞算法的Python实现
- 博客园 - 本科多项式列表
正文
流密码:初入门道
最基础的流密码可以概括为:使用一个保密的短密钥作为种子,通过一个伪随机数生成器制造出一条长长的、一次性的密钥流,然后用这个密钥流与明文进行异或操作来完成加解密。
(当然,这段话像是数学家说的)
- 伪随机数生成器PRG也即密钥流生成器
流密码的流程可表示成下面的TEXT图表:
(加密方)
+---------------------------+
密钥 ----->| 伪随机数生成器 (PRG) |-----> 密钥流 (Keystream)
+---------------------------+ |
V
XOR <---- 明文 (Plaintext)
|
V
密文 (Ciphertext)(解密方)
+---------------------------+
密钥 ----->| 伪随机数生成器 (PRG) |-----> 密钥流 (Keystream) <-- (与加密方生成的一模一样)
+---------------------------+ |
V
XOR <---- 密文 (Ciphertext)
|
V
明文 (Plaintext)为了保证流加密的安全性,PRG必须是不可预测的。弱算法包括
glibc random()函数,线性同余生成器(linear congruential generator)等。
| 类别 (Category) | 典型例子 (Typical Examples) | 核心思想 (Core Idea) | 备注 (Remarks) |
|---|---|---|---|
| 专用的流密码 | ChaCha20 | 从零开始设计的专用高速算法 (ARX结构) | 现代首选。软件实现性能优异,安全性高。 |
| RC4 | 字节级的状态变换 | 已攻破,严禁使用。仅作历史参考。 | |
| 使用分组密码构建 | AES-CTR | 加密一个递增的计数器来生成密钥流块 | 现代首选。可并行,安全性依赖于底层分组密码(AES)的安全性。 |
| AES-OFB | 将加密输出反馈给自身作为下一轮输入 | 无法并行,通常性能不如CTR模式。 | |
| 使用哈希函数构建 | SHA-256-CTR | 对一个递增的计数器进行哈希运算来生成密钥流块 | 安全性依赖于哈希函数的安全性。在协议中已有哈希函数实现时,可节省代码空间。 |
| 不安全的例子 | 线性同余生成器 (LCG) | 简单的线性迭代公式: | 完全不安全,输出是可预测的。 |
glibc random() | 复杂的线性反馈移位寄存器 (LFSR) 变体 | 完全不安全,并非为密码学设计,状态可被轻易恢复。 | |
| 而课本所介绍的线性反馈移位寄存器是一种具有良好统计特性、硬件实现效率极高,但因其“线性”本质而导致密码学上不安全的PRG构建模块 |
现在,让我们转入编程,尝试程序实现一个基于单个LSFR的流密码:
构建玩具流密码
移位寄存器是流密码产生密钥流的一个主要组成部分
描述移位寄存器的反馈模式的函数可表述如下:
考虑到原生Python(不考虑Numpy、Sympy等专用数学库)不方便编写本原多项式,我将效仿教材,将
对于
行为应当与队列相似
Python文档中对队列模块的介绍
queue模块实现了多生产者、多消费者队列。这特别适用于消息必须安全地在多线程间交换的线程编程。模块中的Queue类实现了所有所需的锁定语义。
本模块实现了三种类型的队列,它们的区别仅仅是条目的提取顺序。 在 FIFO 队列中,先添加的任务会先被提取。 在 LIFO 队列中,最近添加的条目会先被提取 (类似于一个栈)。 在优先级队列中,条目将保持已排序状态 (使用heapq模块) 并且值最小的条目会先被提取。
from typing import List, Literal, LiteralString, Any, Callable, Union
from loguru import logger
from colorama import init, Fore, Style
from rich import print as rprint; from rich.markdown import Markdown
from rich.console import Console
from numba import jit, njit
from numba.experimental import jitclass
import numba as nb
init(autoreset=True)
console = Console()
cprint = console.print
from collections import deque
from functools import lru_cache, reduce
from operator import xor
def xor_sum(iterable: List[int]) -> int:
'''
计算一个整数列表的异或和
:param iterable: 输入的整数列表
:return: 返回异或和
:rtype: int
'''
return reduce(xor, iterable, 0)
class StreamKeysV1(deque): # 利用Queue的原生FIFO特性
'''
一个基于单个LSFR的密钥流生成器
:param self: 实例本身
:param polynomial: 本原多项式,你需要哪一位比特参与运算,就让哪一位为1,不参与运算的位为0
例如,polynomial='011001'表示第2、3、6位参与异或运算,第1、4、5位不参与运算
:type polynomial: str
:param initial_state: 初始状态序列,例如[1, 0, 1]表示初始状态序列为a1=1, a2=0, a3=1,
无需在意教材上的反直觉顺序,因为deque会自动处理好顺序问题
:type initial_state: list[int]
'''
# 密钥流生成器
# 需要一个本原多项式和一个初始状态序列
def __init__(self,
polynomial: str, # 本原多项式
initial_state: list[int], # 初始状态序列
):
'''
初始化密钥流生成器
:param self: 实例本身
:param polynomial: 本原多项式,你需要哪一位比特参与运算,就让哪一位为1,不参与运算的位为0
例如,polynomial='011001'表示第2、3、6位参与异或运算,第1、4、5位不参与运算
:type polynomial: str
:param initial_state: 初始状态序列,例如[1, 0, 1]表示初始状态序列为a1=1, a2=0, a3=1,
无需在意教材上的反直觉顺序,因为deque会自动处理好顺序问题
:type initial_state: list[int]
'''
self._period: int = 0 # 密钥流周期
self._is_period_computed: bool = False # 是否已经计算得到周期
# 保留一份初始状态序列的副本
self._initial_state = initial_state.copy()
super().__init__(initial_state)
self.polynomial = polynomial
# 提前生成抽头索引序列,这样就不会在每次更新时都重新计算抽头索引了
self._tap_indices = [
idx for idx, switch in enumerate(polynomial) if switch == '1'
]
if len(self) != len(polynomial):
raise ValueError('初始状态序列和本原多项式长度应当相等')
self._stream = []
def _calc_period(self) -> None:
while not self._is_period_computed:
self._period += 1
self._update()
if list(self) == self._initial_state:
self._is_period_computed = True
# logger.info(f'密钥流周期计算完毕,周期为 {self._period}')
@property
def period(self) -> int:
'''
返回密钥流的周期;密钥流的周期会在生成密钥流时进行统计,这意味着密钥流生成的不够大时,
程序可能得不到正确的密钥周期
:return: 密钥流的周期
:rtype: int
'''
if not self._is_period_computed:
self._calc_period()
return self._period
def _update(self) -> int:
'''
更新状态序列——简单地说,是根据ploynomial判断状态序列的哪几位会参与异或运算
异或运算得到的结果会被append到状态序列的右端,同时pop出最左边的值作为该
函数的副作用产物
:param self: 实例本身,这里即deque序列,直接获取值序列
:return: 返回int类型的被pop出来的值
:rtype: int
'''
# TODO: 优化列表推导式性能,考虑使用位运算或预计算索引
picked_iterables = [
self[idx] for idx in self._tap_indices
]
temp_output = xor_sum(picked_iterables) # 对检索出来的序列进行异或运算
self.append(temp_output)
return self.popleft() # 弹出最左端的值
def _reset(self) -> None: # 重置状态序列
self.clear()
init_state = self._initial_state.copy()
self.extend(init_state)
def stream(self) -> Any:
# 更换为使用迭代器产生每一位密钥
try:
while True:
yield self._update()
finally: # 退出生成器时重置状态序列
self._reset()
def get_stream(self) -> List[int]:
'''
生成密钥流,返回一个列表;密钥流长度不会大于周期,因此,如果要获取与明文一样的较长密钥流,
请配合itertools.Cycle使用,使用示例如下:
>>> from itertools import cycle
>>> long_key_stream = [next(cycle(stream.get_stream())) for _ in range(plaintext_length)]
:param expected_length: 期望的密钥流长度
:type expected_length: int
:return: 返回一个包含密钥流的列表
:rtype: List[int]
'''
self._reset() # 每次生成密钥流前都重置状态序列
return [self._update() for _ in range(self.period)]
self._reset()
def __repr__(self) -> str:
return super().__repr__()
if __name__ == '__main__':
from random import randint
from time import time
stream = StreamKeysV1(
polynomial='1000010000001000', # 这里只是占位,避免报错
# x^{16} + x5 + x^{3} + x + 1
initial_state=
[randint(0, 1) for _ in range(16)]
)
# google搜索给出的多项式不能直接进行十六进制转二进制,而应该根据我这里的算法取出实际参与运算的索引
stream._tap_indices = [15, 4, 2, 0] # 直接覆盖抽头索引
cprint(stream)
# 测试状态序列更新
for i in range(10):
output = stream._update()
logger.info(f'更新状态序列,当前状态序列: {list(stream)}, 弹出值: {output}')
stream._reset()
# 生成密钥流
t1 = time()
key_stream = stream.get_stream()
t2 = time()
logger.info(f'密钥流: {''.join(
[str(bit) for bit in key_stream]
)} 周期为 {stream.period}')
logger.info(f'生成密钥流(同时计算周期)耗时 {(t2 - t1) * 1000} 毫秒')
for _ in range(5):
t1 = time()
# 再次生成,但这次应该不会再重复计算周期了
key_stream = stream.get_stream()
t2 = time()
# 直接打印耗时
logger.info(f'二次生成密钥流耗时 {(t2 - t1) * 1000} 毫秒')010001000110101000011101101111010010000011101101001101101111001100000011111101 周期为 65535
2025-10-02 21:38:13.273 | INFO | __main__:<module>:214 - 生成密钥流(同时计算周期)耗时 72.34454154968262 毫秒
2025-10-02 21:38:13.301 | INFO | __main__:<module>:221 - 二次生成密钥流耗时 27.640581130981445 毫秒
2025-10-02 21:38:13.328 | INFO | __main__:<module>:221 - 二次生成密钥流耗时 26.445865631103516 毫秒
2025-10-02 21:38:13.356 | INFO | __main__:<module>:221 - 二次生成密钥流耗时 27.601957321166992 毫秒
2025-10-02 21:38:13.381 | INFO | __main__:<module>:221 - 二次生成密钥流耗时 25.506258010864258 毫秒
2025-10-02 21:38:13.410 | INFO | __main__:<module>:221 - 二次生成密钥流耗时 28.684616088867188 毫秒代码实现时继承了deque(一个双向队列类),当然,不继承也没啥,这里只是想利用deque的pop方法和append方法尽可能节省性能开销罢了:
class StreamKeysV1(deque): # 利用Queue的原生FIFO特性
def __init__(self,
polynomial: str, # 本原多项式
initial_state: list[int], # 初始状态序列
):
pass为便于理解,这里将initial_state属性标注为list[int]整型列表,实际使用时不需要关心参数的传递顺序(是从序列左侧到右侧,还是从右侧到左侧)
def __init__(self,
polynomial: str, # 本原多项式
initial_state: list[int], # 初始状态序列
):
self._period: int = 0 # 密钥流周期
self._is_period_computed: bool = False # 是否已经计算得到周期
# 保留一份初始状态序列的副本
self._initial_state = initial_state.copy()
super().__init__(initial_state)
self.polynomial = polynomial
# 提前生成抽头索引序列,这样就不会在每次更新时都重新计算抽头索引了
self._tap_indices = [
idx for idx, switch in enumerate(polynomial) if switch == '1'
]
if len(self) != len(polynomial):
raise ValueError('初始状态序列和本原多项式长度应当相等')定义一些属性以备后续使用。这里进行了抽头索引的预处理:
self._tap_indices = [
idx for idx, switch in enumerate(polynomial) if switch == '1'
]对于110的多项式字符串,会得到这样的索引序列:
>>> [1, 1, 0]从左到右直接映射到
(早先的版本还是按照
def _update(self) -> int:
picked_iterables = [
self[idx] for idx in self._tap_indices
]
temp_output = xor_sum(picked_iterables) # 对检索出来的序列进行异或运算
self.append(temp_output)
return self.popleft() # 弹出最左端的值接下来是状态更新原子操作,根据上面的抽头序列从self实例取出对应位置的01值,然后进行异或运算。这里的xor_sum其实和sum没关系,只是封装了一下reduce函数,用operator.xor作为reduce的回调参数处理传给它的抽头01值。得到异或值添加到队列右边,也就是下标大的一侧(对于
原子化状态更新操作后就可以组装密钥流生成函数了:
def get_stream(self) -> List[int]:
self._reset() # 每次生成密钥流前都重置状态序列
return [self._update() for _ in range(self.period)]直接用列表推导式一步到位
也可以计算周期(同样是全量进行):
def _calc_period(self) -> None:
while not self._is_period_computed:
self._period += 1
self._update()
if list(self) == self._initial_state:
self._is_period_computed = True
# logger.info(f'密钥流周期计算完毕,周期为 {self._period}')
@property
def period(self) -> int:
'''
返回密钥流的周期
:return: 密钥流的周期
:rtype: int
'''
if not self._is_period_computed:
self._calc_period()
return self._period这里使用了@property装饰period函数,这是Python中的getter写法。前面生成密钥时如果周期尚未完成计算,那么会先进行周期计算,然后才生成密钥流——因此,生成器会存在一个冷启动的耗时
冷启动的耗时还是蛮大的,近乎两倍于生成密钥流的耗时(二者都涉及一整个周期的状态更新操作,但冷启动还包括多次list创建开销……)
品鉴无优化版本的性能
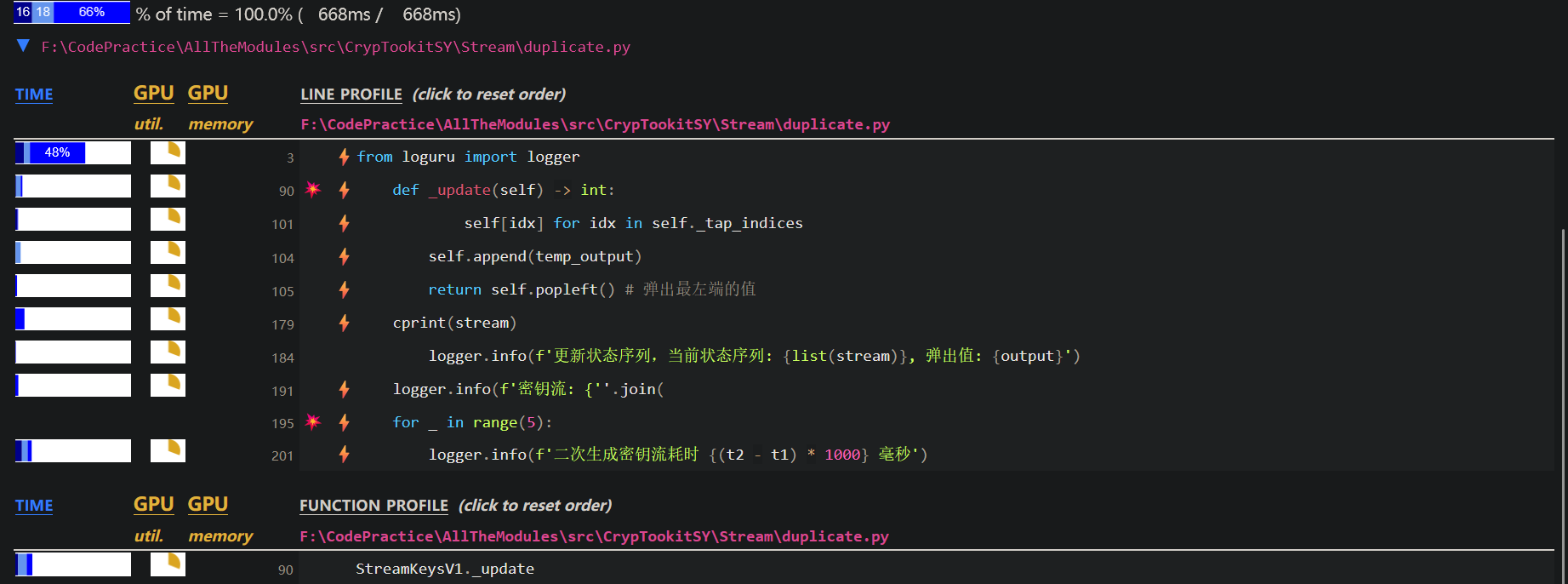
上面那玩意的性能开销还是很恐怖的,特别是计算周期时重复创建列表……
python -m cProfile src\CrypTookitSY\Stream\duplicate.py > performence.txt
# cProfile是内置工具让我们品鉴一下这份报告
Gemini生成
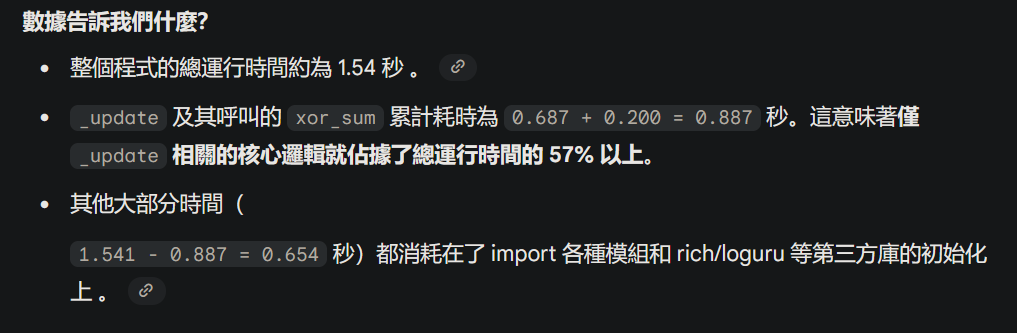
從cProfile的輸出中,我們關注cumtime(累計時間)和ncalls(呼叫次數)最高的幾個關鍵函式:
duplicate.py:90(_update):呼叫次數 (ncalls): 458,755 次 (七次全周期状态更新,其中包括计算周期本身产生的一次全周期状态更新)
累計時間 (cumtime): 0.687 秒
分析: 這是最主要的瓶頸。
_update函式被呼叫了超過45萬次,佔據了整個程式運行時間的很大一部分。每一次呼叫都涉及到列表推導、函式呼叫和deque操作,這些在高頻率呼叫下成本非常高。
duplicate.py:18(xor_sum):呼叫次數 (ncalls): 458,755 次
累計時間 (cumtime): 0.200 秒
分析:
xor_sum被_update函式等量呼叫,是第二大瓶頸。它內部使用的reduce函式(被呼叫458,755次,總耗時0.110秒)本身效率不低,但「準備資料」和「函式呼叫」的成本疊加起來就非常可觀了。
內建的
deque方法:{method 'append' of 'collections.deque' objects}: 呼叫了 458,755 次,總耗時 0.055 秒 5。{method 'popleft' of 'collections.deque' objects}: 呼叫了 458,755 次,總耗時 0.053 秒 6。分析: 雖然
deque的append和popleft本身是 O(1) 操作,非常高效,但在近50萬次的呼叫下,它們的總耗時也達到了約100毫秒,成為了不可忽視的成本。
duplicate.py:69(_calc_period):呼叫次數 (ncalls): 1 次
累計時間 (cumtime): 0.134 秒
分析: 儘管
_calc_period只被呼叫了一次,但它內部迴圈呼叫了_update,導致了顯著的累計耗時。這清晰地顯示了首次運行的成本主要來自於此。
uv add scalene现在看到scalene的分析报告,爆点显然也是那个_update函数
位运算重构
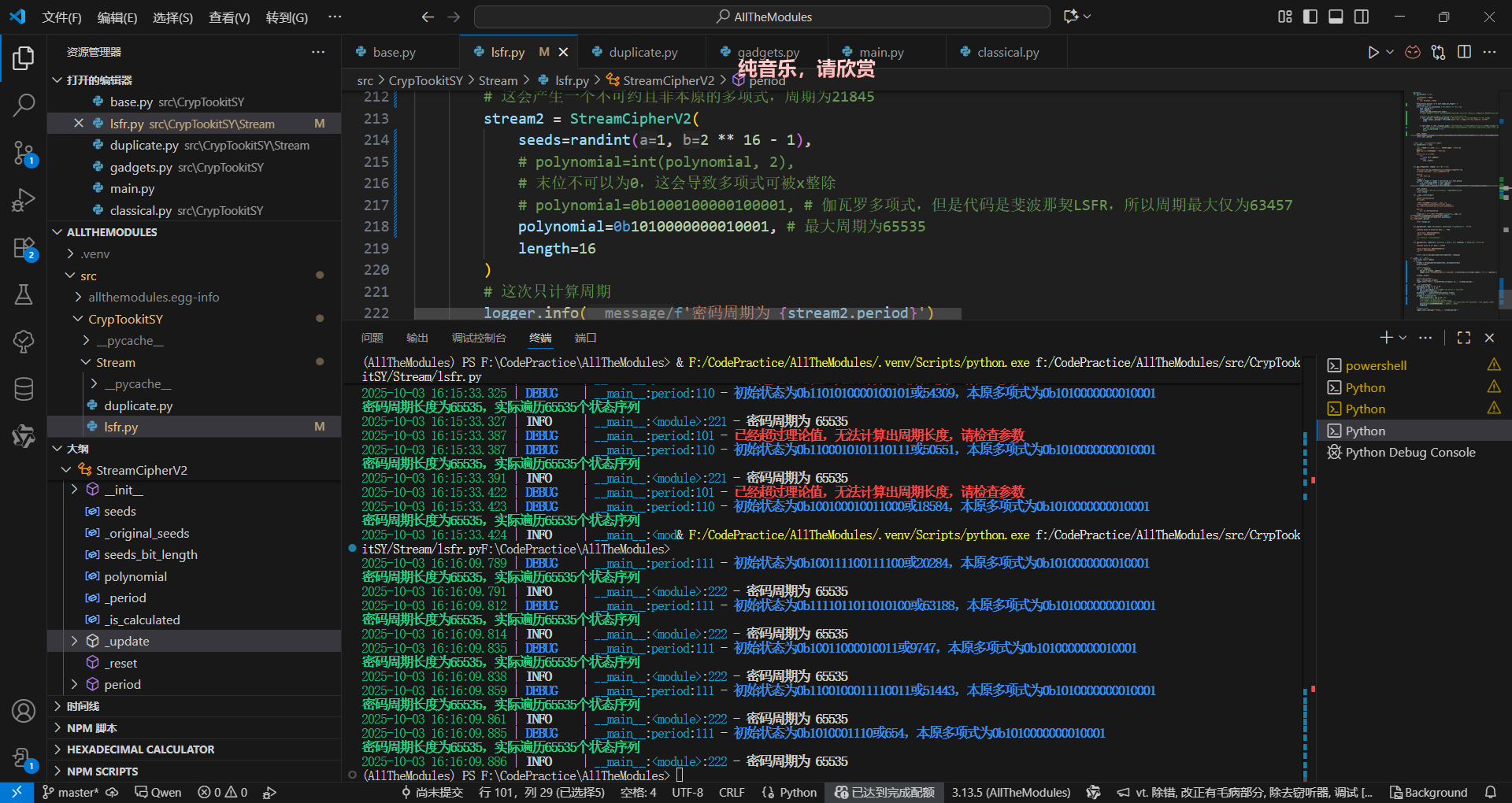
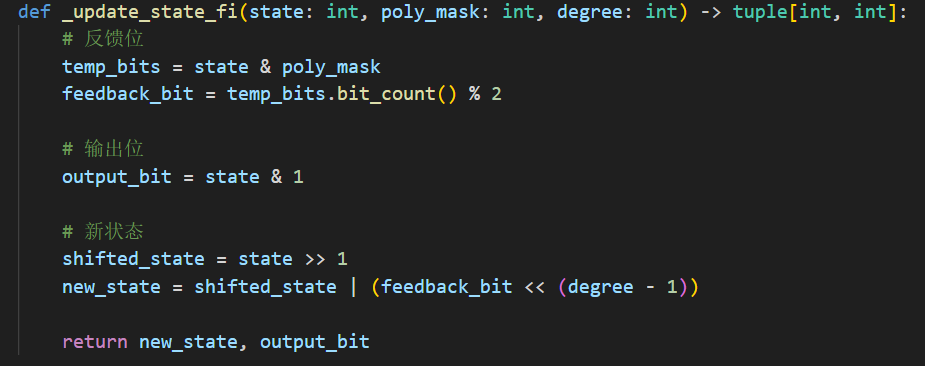
def _update_state_fi(state: int, poly_mask: int, degree: int) -> tuple[int, int]:
# 反馈位
temp_bits = state & poly_mask
feedback_bit = temp_bits.bit_count() % 2
# 输出位
output_bit = state & 1
# 新状态
shifted_state = state >> 1
new_state = shifted_state | (feedback_bit << (degree - 1))
return new_state, output_bit
def _calc_period_fi(state: int, poly_mask: int, degree: int) -> tuple[bool, int, int]:
expected_max_period = 2**degree - 1
visited_rouds = 0
original_state = state; next_state = state
while True:
next_state, _ = _update_state_fi(state=next_state, poly_mask=poly_mask, degree=degree)
visited_rouds += 1
# print(visited_rouds)
if next_state == original_state:
return True, visited_rouds, next_state
# 注意返回最新的状态
if visited_rouds > expected_max_period:
return False, visited_rouds, next_state
class LSFRCore:
def __init__(
self,
seed: int,
polynomial: int, # 多项式抽头掩码
degree: int = -1, # 多项式项数
):
self._seed = seed
self._initial_state = seed
self.state = self._initial_state
"""
n比特的状态整数, 约定最低位代表a_1,最高位代表a_n
"""
self._polynomial = polynomial
"""
n比特的多项式掩码整数, 约定最低位为c_n, 最高位为c_1
"""
self._polynomial_degrees = degree if degree > 0 else polynomial.bit_length() - 1
"""
多项式掩码次数, 决定了多项式的理论最大周期, 即2^{degree} - 1;
决定掩码大小, 以便舍弃状态序列的高位\n
亦可决定LSFR长度;
~~特征多项式阶数与这里的掩码次数并不等同~~
"""
self.lsfr_width = self._polynomial_degrees
self._period = 0
self._is_calculated = False # 是否已经计算过周期,初始为False
# 二次校验 舍去高位比特
self.mask = (1 << self.lsfr_width) - 1
self.state = self.state & self.mask
self._initial_state = self.state & self.mask
"""
舍弃状态序列高位,只保留LSFR位宽长度的低比特
"""
@property
def period(self) -> int:
if not self._is_calculated:
self._is_calculated, self._period, self.state = _calc_period_fi(
self.state, self._polynomial, self._polynomial_degrees
)
if not self._is_calculated: # 如果没有计算成功,则返回一个错误信息
# logger.error(f'LSFR周期计算失败,请检查多项式掩码是否正确,或者尝试使用更长的状态序列')
pass
return self._period
def keys(self, length: int = 0) -> tuple[list[int], int]:
_keys, final_state = _get_stream_fi(length,
state=self.state,
poly_mask=self._polynomial,
degree=self._polynomial_degrees
)
self.state = final_state
_keys = int(f'{_keys}'[1:-1].replace(', ', ''), 2)
return _keys
def reset(self) -> None:
self.state = self._initial_state
@property
def poly(self) -> int:
return self._polynomial
@poly.setter
def poly(self, value: int) -> None:
if value <= 1:
raise ValueError("多项式掩码必须为不小于或等于1的正整数")
if value == self._polynomial:
return # 没有改变
self._polynomial = value
self._polynomial_degrees = value.bit_length() - 1
# 重置LSFR并对状态进行高位截断
self.lsfr_width = self._polynomial_degrees
mask = (1 << self.lsfr_width) - 1
# 舍去状态序列的高位
self._initial_state = self._initial_state & mask
self.state = self.state & mask
# 重置周期计算
self._is_calculated = False
def __repr__(self, **kwargs) -> str:
return f'<斐波那契LSFR核心架构{self.__class__.__name__} 多项式掩码为{bin(self.poly)} LSFR位宽为{self.lsfr_width} 状态序列为{bin(self.state)} 周期为{self.period}>'
class FiLSFR(LSFRCore):
def __init__(
self,
seed: int | bytes | bytearray | str, # 状态序列
polynomial: int | bytes | bytearray | str, # 多项式抽头掩码
degree: int = -1, # 多项式项数
order: str = 'big',
encoding: str | None = None, # 字符串编码时的字符集
):
# 如果输入字符串就先编码
seed = seed.encode(encoding=encoding) if isinstance(seed, str) else seed
polynomial = polynomial.encode(encoding=encoding) if isinstance(polynomial, str) else polynomial
'''if isinstance(seed, int) and order == 'little':
seed = reverse_int_by_bit(seed, bitwidth=8)
if isinstance(polynomial, int) and order == 'big':
polynomial = reverse_int_by_bit(polynomial, bitwidth=1)'''
# 完全信任用户,如果用户给的是int那就用int
# 不行的话按字节序列处理
if isinstance(seed, bytes) and order == 'little':
seed = seed[::-1]
seed = int.from_bytes(seed, order)
if isinstance(polynomial, bytes) and order == 'big':
polynomial = polynomial[::-1]
polynomial = int.from_bytes(polynomial, order)
super().__init__(seed, polynomial, degree)
def _update(self):
next_state, output_bit = _update_state_fi(state=self.state, poly_mask=self.poly, degree=self.lsfr_width)
self.state = next_state
return output_bit
def _stream_bytes(self):
self.reset() # 重置状态
while True:
byte = 0
for _ in range(8): # 一次导出八位比特
byte = byte << 1 | self._update()
yield byte
# 加解密器依赖Pycryptodome库的函数进行字节编码
def encrypt(self, data: Union[bytes, bytearray], order='big') -> bytes:
key_gen = self._stream_bytes()
return bytes(byte ^ key for byte, key in zip(data, key_gen))
def decrypt(self, ciphertext: bytearray | bytes, order='big') -> bytes:
key_gen = self._stream_bytes()
return bytes(byte ^ key for byte, key in zip(ciphertext, key_gen))
class FiLSFRV2(FiLSFR):
def __init__(self, compatible: bool = False, **kwargs):
super().__init__(**kwargs)
mask = 2**self._polynomial_degrees - 1
if not compatible:
self.poly &= mask # 舍去最高位,最高位只用于决定多项式次数位运算逻辑阐述
注意
V2版本的诸多问题在V4才有修复或改善
def __init__(
self,
seed: int | bytes | bytearray | str, # 状态序列
polynomial: int | bytes | bytearray | str, # 多项式抽头掩码
degree: int = -1, # 多项式项数
order: str = 'big',
encoding: str | None = None, # 字符串编码时的字符集
):
...seed和polynomial的含义不多赘述。degree属性指LSFR寄存器宽度(也指多项式的bits),计算方式如下:
self._polynomial_degrees = degree if degree > 0 else polynomial.bit_length() - 1
"""
多项式掩码次数, 决定了多项式的理论最大周期, 即2^{degree} - 1;
决定掩码大小, 以便舍弃状态序列的高位\n
亦可决定LSFR长度;
~~特征多项式阶数与这里的掩码次数并不等同~~
"""
self.lsfr_width = self._polynomial_degrees即多项式长度-1——LSFR长度看的是多项式的次数,而不只是二进制多项式序列 的位宽order属性的作用我们后面会回顾到的
所以为什么n-bits多项式是n+1位二进制?
答案的核心在於:一個 n 次多項式總共有 n+1 個係數,包括從
一個通用的 n 次多項式,其最完整的數學表達式是這樣的:
- ...
1)項的係數。
係數的下標是從 0 到 n。所以總個數是 $$(n−0)+1=n+1 $$
在 GF(2) 域中,每一個係數 aᵢ 的值只可能是 0 或 1。這意味著,要完整地表示這個多項式,我們需要 n+1 個比特位,每一個比特位用來記錄對應項的係數是 0 還是 1。
那么從數學到二進位的映射,最直觀的映射方式就是,讓 k 位(從0開始數)
2025-10-04T17:08:51.701217+0800 INFO 获得 3-bit 本原多项式为: 1011用日誌中的 3 次本原多項式為例:
- 數學形式: $$P(x)=x^3+x+1$$
- 寫出完整形式: 為了看得更清楚,我們把所有係數都寫出來:
- 提取係數: 按照從高到低的順序,我們得到一組係數 $$(a3,a2,a1,a0)=(1,0,1,1)$$
- 計數: 總共有
- 映射為二進位: 將這組係數直接寫成二進位序列,就得到了
1011。
結論:因此,一個 3 次多項式,需要 4 位二進位序列1011來完整表示。
多项式序列最高位仅决定多项式的次数,不决定LSFR长度:
class FiLSFRV2(FiLSFR):
def __init__(self, compatible: bool = False, **kwargs):
super().__init__(**kwargs)
mask = 2**self._polynomial_degrees - 1
if not compatible:
self.poly &= mask # 舍去最高位,最高位只用于决定多项式次数接下来看到状态更新(原子操作)逻辑:
def _update_state_fi(state: int, poly_mask: int, degree: int) -> tuple[int, int]:
# 反馈位
temp_bits = state & poly_mask
feedback_bit = temp_bits.bit_count() % 2
# 输出位
output_bit = state & 1
# 新状态
shifted_state = state >> 1
new_state = shifted_state | (feedback_bit << (degree - 1))
return new_state, output_bit这里,我将状态序列的最高位视为
如果将状态序列从左到右映射到
- 计算状态序列的位宽
- 将掩码1左移到
位宽-1位 - 用这个高位掩码对状态序列进行与运算,得到LSFR所推出的值
涉及位宽计算(bit_count()函数)、一次左移和一次与运算,直观,但不高效
而将最低位视为
output_bit = state & 1然后计算反馈函数值:
首先,我们计算出
然后对这个序列进行奇偶校验 得到反馈函数值。在一开始的构想我称之为类似逐个求和的逐位线性异或 操作
但,多个数值进行异或求和操作时,决定最终结果的显然就是这个数值序列中1的个数
奇偶校验位(英语:Parity bit)或校验比特(check bit)是一个表示给定位数的二进制数中1的个数是奇数还是偶数的二进制数。奇偶校验位是最简单的错误检测码。
这里进行奇偶校验并不是要对状态序列进行纠错,而是要获得奇偶校验的中间值,也就是定位数的二进制数中1的个数是奇数还是偶数,然后对2求模,得到
# 反馈位
temp_bits = state & poly_mask
feedback_bit = temp_bits.bit_count() % 2这里使用了int类型的bit_count()函数,函数是C实现的,性能自然不必多问
最后将
# 新状态
shifted_state = state >> 1
new_state = shifted_state | (feedback_bit << (degree - 1))把F值左移到LSFR状态最高位,然后与舍弃最低位的状态序列进行或运算即可
关于状态序列和多项式序列的比特顺序
正所谓大端序是符合人类直觉的写法,小端序是反人类的写法——我说的
在上面演示的代码中,状态序列和多项式序列在进入LSFR原子状态更新操作前都没有进行逆置操作,是完全一比一映射到反馈函数上的,因此状态序列实际上(从最高位到最低位)映射的是
当然一个本原多项式在正确的LSFR实现下理论上可以用状态机遍历所有
不同类型的多项式
重新认识多项式
注意
繁体中文警告。Gemini犯傻了,我有点管不住
首先,讓我們回到中學數學。一個多項式(Polynomial)就是這樣一個表達式:
x是一個變數。a_n, a_{n-1}, \dots這些是係數 (coefficients),在傳統數學裡它們是實數、整數等。n是多項式的次數 (degree),即x的最高次冪。
例如,
但在密碼學中,我們對多項式的用法完全不同。 我們要先把它從我們熟悉的數字世界,「移植」到一個特別的、更簡單的「數字宇宙」裡。
密碼學中的運算,尤其是對稱密碼,幾乎都發生在有限域 (Finite Field) 或稱伽羅瓦域 (Galois Field) 中。對我們討論的流密碼而言,這個「宇宙」就是 GF(2)。
這個 GF(2) 宇宙有兩條非常簡單的根本法則:
- 僅有的元素: 世界上只有兩個「數字」:0 和 1。
- 新的運算規則:
- 加法
+變成了異或⊕(XOR)。 (例如: 1+1=1⊕1=0)(或曰模2加法,不进位) - 減法
-也變成了異或⊕。 (因為 a⊕a=0) (或曰模2减法,不借位) - 乘法
*變成了與&(AND)。 (例如: 1∗1=1,1∗0=0)
- 加法
現在,當我們把多項式移植到這個宇宙,它就變成了GF(2) 上的多項式。這意味著:
- 所有係數
a_i只能是 0 或 1。 - 多項式之間的加減法都變成了異或運算。
例如,我們之前討論的本原多項式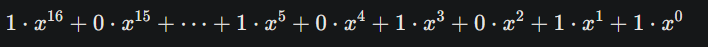
在 GF(2) 上的多項式不再是用來畫圖或解方程的。它變成了一種抽象的代數工具,密碼學家們用它來: - 定義規則。
- 構造更複雜的數學系統。
在整個密碼學領域,多項式扮演著好幾個至關重要的角色:
A. 構造更大的有限域 (最重要的作用)
這就是AES 加密演算法的核心基礎。AES 演算法的所有運算都在一個包含 28=256 個元素的有限域 GF(28) 中進行。而這個 GF(28) 宇宙本身,就是通過一個8次的不可約多項式在 GF(2) 的基礎上構造出來的。簡而言之,多項式是建造更高級密碼運算「場地」的藍圖和工具。
B. 纠错码 (Error-Correcting Codes)
像里德-所羅門碼 (Reed-Solomon codes) 這類技術,廣泛應用於 QR Code、光碟儲存等。它們使用多項式對數據進行編碼,即使部分數據在讀取或傳輸中出錯,也可以利用多項式的數學特性「反解」出原始的正確數據。
C. 公钥密码学 (Public-Key Cryptography)
橢圓曲線密碼學 (ECC):定義一條橢圓曲線的方程 y2=x^{3}+ax+b 本身就是一個多項式方程。所有運算都在這個多項式定義的曲線上進行。
後量子密碼學 (PQC):許多被看好的後量子密碼方案,如基於格 (Lattice-based) 的密碼學,其核心運算就是在「多項式環」上進行的,比單純的數字運算更複雜也更安全。
D. 秘密分享 (Secret Sharing)
夏米爾秘密分享方案 (Shamir's Secret Sharing) 是一個絕妙的例子。要把一個秘密 S 分給 n 個人,讓其中任意 k 個人湊在一起才能解鎖,是這樣做的:
隨機構造一個
k-1次多項式,讓它的常數項 a0=S。在這個多項式的曲線上取
n個不同的點 (x1,y1),(x2,y2),…。每個人分到一個點的座標。
由於「k個點可以唯一確定一個k-1次多項式」的數學原理,只有集齊了 k 個點(k個人)才能還原整個多項式,從而得到秘密 a0。
這正是您在過去两天裡一直在親手實踐和調試的部分。在流密碼(特指基於LFSR的流密碼)這個狹義的語境下:
多項式的唯一作用,就是充當 LFSR 的「狀態轉移規則」或「基因藍圖」。
這個角色非常具體:
- 定義連接 (Taps):多項式的每一個項(例如
- 定義反饋邏輯 (Feedback Logic):整個多項式定義了哪些抽頭的位需要被收集起來,進行異或運算,以產生下一時刻要注入寄存器的新位元。
在這個作用下,多項式的「好壞」就顯得至關重要,這也就是我們之前詳細討論的:
- 可約多項式 (Reducible):一張「破碎的」藍圖,導致LFSR的狀態機分裂成多個短循環,產生的金鑰流序列短且重複,毫無安全性可言。
- 不可約多項式 (Irreducible):一張「合格的」藍圖,能保證LFSR的狀態構成一個或多個完整的長循環。
- 本原多項式 (Primitive):一張「完美的」藍圖,它能保證LFSR發揮最大潛能,將所有非零狀態串聯成一個單一的、長度達到理論極限
可以這樣理解:多項式本身是一個源自基礎數學的工具,但在密碼學家手中,它被賦予了新的生命。在宏觀上,它是構建各種密碼系統(如AES、ECC)的基礎建材;而在流密碼這個微觀的角落,它則扮演著一個極其專注的角色——為LFSR這個序列產生引擎提供最核心的、決定其序列品質的遺傳密碼。
可约、本原:如何描述一个多项式的性能
可约和本原这两个概念是评价一个多项式能否用于密码学序列生成的基础,它们直接决定了状态序列的结构和质量
可约多项式 (Reducible Polynomial)
- 核心行为特征:分裂、短小、不可靠
- 具体影响:
- 状态空间分裂 (Fractured State Space):这是最致命的问题。它会将LFSR的所有非零状态分割成多个互不连通的、规模不等的小循环。
- 周期依赖于初始状态:LFSR最终的周期完全取决于其初始状态(种子)恰好落在了哪个小循环里。不同的种子会产生长度完全不同、序列也完全不同的短周期。
- 状态覆盖率极低:在任何一次运行中,LFSR只能遍历所有可能状态中的一小部分。
- 对流密码的影响:完全不可用。产生的密钥流序列短、重复性强、且极易被预测。它不具备任何伪随机性,无法提供安全性。
本原多项式 (Primitive Polynomial)
- 核心行为特征:完整、最长、确定性
- 具体影响:
- 单一巨大循环 (Single Maximal Cycle):它能保证将LFSR的所有
- 周期与初始状态无关:只要初始状态不是全零,无论选择哪个初始状态,最终产生的序列周期永远是理论最大值
- 状态覆盖率100%:一次完整的周期会不重复地遍历所有非零状态。
- 单一巨大循环 (Single Maximal Cycle):它能保证将LFSR的所有
- 对流密码的影响:理想的构建模块。它生成的序列(称为
- 均衡性:在一个周期内,
1的个数比0的个数仅多一个。 - 游程特性:序列中连续
1或连续0的“段落”分布规律接近真随机。 - 自相关性:序列与其移位后的版本,相关性极低。 这些特性使得其输出的密钥流难以被统计分析破解,是LFSR型流密码安全性的基础。
- 均衡性:在一个周期内,
其他性能指标
除了“可约性”和“本原性”这两个决定周期结构的根本指标外,在工程实践中,密码学从业人员还关心以下几个重要指标:
- 项数 (Number of Terms) / 稀疏性 (Sparsity)
- 指标含义:多项式中系数为
1的项的个数。项数越少,多项式越“稀疏”。 - 为何重要:它直接决定了LFSR硬件或软件实现的计算性能(速度)。
- 三项式 (Trinomial):形式为
- 五项式 (Pentanomial):形式为
- 稠密多项式:项数很多,需要的异或运算也更多,速度相对较慢。
- 三项式 (Trinomial):形式为
- 对流密码的影响:在保证“本原性”的前提下,密码学家和工程师会优先选择本原三项式或本原五项式,以实现最高的密钥流生成速度。
- 指标含义:多项式中系数为
- 不可约但非本原 (Irreducible but not Primitive)
- 指标含义:这本身是一种多项式类型,其关键性能指标是它所生成的循环长度(阶)。
- 为何重要:它虽然不能产生最大长度周期,但能保证状态空间不分裂,产生一个长度为 2n−1 的某个因子的稳定周期。
- 您之前测试得到的
21,845和63,457都是这种情况。
- 您之前测试得到的
- 对流密码的影响:在严格的密码学应用中,我们几乎总是要求最大周期,所以这类多项式通常不被选用。但在某些非密码学应用(如通信中的数据扰码、测试序列生成)中,如果其周期足够长,也可能会被使用。
- 线性复杂度 (Linear Complexity)
- 指标含义:对于一个序列,能够生成它的最短LFSR的长度。对于一个由n次本原多项式产生的m序列,其线性复杂度就是
n。 - 为何重要:这是衡量一个序列抗代数攻击能力的核心指标。著名的Berlekamp-Massey算法可以在知道
2n个连续比特的情况下,反推出这个n位的LFSR结构。 - 对流密码的影响:为了保证安全性,流密码的线性复杂度必须非常大。这意味着LFSR的长度
n必须足够大(例如128, 256位)。一个16位的LFSR,即使使用了最好的本原多项式,其线性复杂度也只有16,可以被瞬间破解。因此,现代流密码要么使用很长的LFSR,要么(更常见地)将多个LFSR或非线性函数组合起来,以获得远超单个LFSR长度的、巨大的线性复杂度。
- 指标含义:对于一个序列,能够生成它的最短LFSR的长度。对于一个由n次本原多项式产生的m序列,其线性复杂度就是

注
在我的Python程序实现中,多项式的稀疏性并不会影响程序性能。程序中唯一与稀疏性和异或次数有关的代码是:
# 反馈位
temp_bits = state & poly_mask
feedback_bit = temp_bits.bit_count() % 2
# 输出位
output_bit = state & 1
# 新状态
shifted_state = state >> 1
new_state = shifted_state | (feedback_bit << (degree - 1))bit_count函数的实现是这样的:
- 终极武器:CPU 硬件指令 (
POPCNT)
现代的 CPU(例如支持 SSE4.2 指令集的 x86 架构,以及大多数 ARM 架构)内置了一条名为POPCNT(Population Count) 的硬件指令。
- 作用: 这条指令可以在一个时钟周期内(或极少的几个周期内),计算出一个机器字长(例如64位)的整数中包含多少个
1。 - 实现: CPython 的 C 语言源码在编译时,会检测编译器和目标平台是否支持这个功能(例如通过 GCC/Clang 的
__builtin_popcount内建函数)。如果支持,int.bit_count()的调用最终就会被编译成这条单一的、快如闪电的机器码指令。
- 高速备选:优化的 C 语言算法
如果 CPU 比较老旧,不支持POPCNT指令,CPython 也会采用高效的 C 语言算法作为备选,而不是简单的逐位检查。最常见的备选方案之一是:
- 查找表法 (Lookup Table):
- 预先计算并存储一个包含256个条目(从0到255)的表,表里是每个8位数字的
bit_count结果。 - 当需要计算一个64位整数的
bit_count时,程序会将其看作8个8位的字节。 - 对每个字节,直接查表得到结果,然后将8个结果相加。 这个方法比循环快得多,因为它用内存访问(查表)替代了大量的位运算和循环判断。
- 预先计算并存储一个包含256个条目(从0到255)的表,表里是每个8位数字的
本原多项式的相关数学定理
注
因为我挂着湾湾梯子,所以Gemini有时候会以为我用繁体中文
存在性与数量定理
定理: 對於任何正整數次數 n,n次本原多項式總是存在的。其總數可以精確計算為:
其中
解讀與驗證:
這個定理告訴我們本原多項式並不罕見,而且其數量有明確的規律。讓我們用之前遍歷找到的 5次 本原多項式的結果來驗證它!
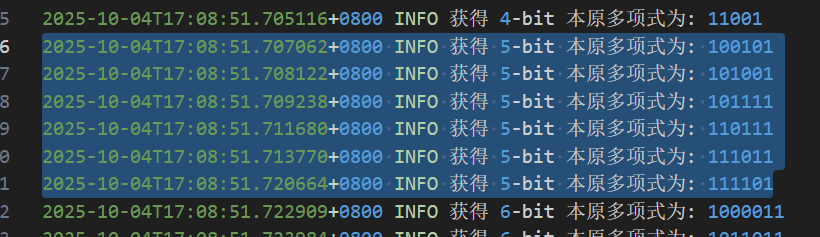

- 對於
n=5,我們需要計算 $$\frac{ϕ(2^5−1)}{5}$$ 31是一個質數。對於一個質數p,- 代入公式:$$數量 = 30/5=6$$
這完美地解釋了為什麼程式在遍歷5次多項式時,不多不少正好找到了6個! 實驗結果與這個數學定理完美地吻合了
- 對於
倒数定理 (Reciprocal Theorem)
定理: 如果
解讀與驗證:
這意味著本原多項式總是「成對出現」(除非一個多項式恰好是自己的倒數,即回文多項式)。

在上一輪的日誌中已經完美地驗證了這一點,所找到的6個5次本原多項式,正好構成了三對互為倒數的「對稱」多項式。
注意

乍一看本原多项式似乎确实是形式对称的,但不要真的这样想当然
奇数项定理 (Odd Number of Terms Theorem)
定理: 任何在 GF(2) 上次數大於1的不可約多項式,其項數(即係數為1的個數)必然是奇數。
解讀與驗證:
因為所有本原多項式首先都必須是不可約的,所以這個定理同樣適用於本原多項式。
為什麼? 這裡有一個簡單的證明:如果一個多項式
1相加(異或)。在GF(2)中,偶數個1異或的結果是0。根據因式定理,如果驗證: 您可以檢查一下您找到的所有本原多項式,例如:
1011(10011(111101(
它們的二進制表示中‘1’的個數必然都是奇數。這個定理可以幫助您在遍歷搜索時,直接跳過所有項數為偶數的多項式,將搜索空間減半!这整个六级小标题的内容是在写完测试代码后才加上的,所以测试代码并没有进行优化
與梅森素數的關係 (Connection to Mersenne Primes)
定理: 如果
解讀與驗證:
在這種特殊情況下,「不可約」和「本原」這兩個概念的界線消失了。只要一個多項式是「不可約」的(性質良好),它就必然是「本原」的(性質最優)。
為什麼? 這源於數量定理。如果
驗證:
n=3时,n=5时,n=4时,
相关信息
我有点晕了
多项式的选取如何影响程序行为
一个不够完美的多项式其循环是什么样的?分裂后有几部分?如何找到它们?
要彻底分析一个n次多项式 P(x) 所决定的LFSR的行为,我们需要遵循以下三个数学步骤:
- 【因式分解】: 将多项式 P(x) 在 GF(2) 域上分解成不可约因子的乘积。
- 【计算阶元】: 对每一个独特的不可约因子 Pi(x),计算它的“阶”(Order)。
- 【合并周期】: 根據所有因子的阶,通过数论方法(最小公倍数)计算出完整的循环结构。
如何计算多项式的理论性能
如何约分一个多项式
以多项式序列0b0101(按照前面的小端序进行解析,得到
相关信息
按照大端序,从0b1010。
笔者注
这一五级标题中多项式序列的映射规则一直在变化,因此文案细节也可能存有谬误
这涉及數學表示法和程式碼實現之间的差异,我将在程序测试一节中深入这个问题
该多项式映射得到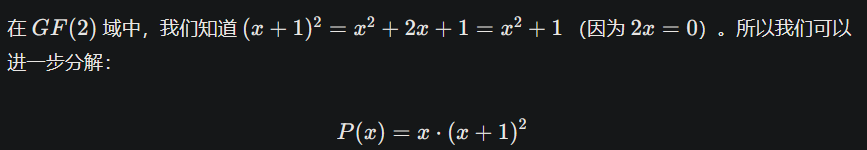
回顾一下GF域中的运算操作
GF(2)的基本法则如下:
- 域中元素:這個宇宙裡只有兩個「數字」:0 和 1。
- 運算規則:
- 加法 (+) 就是 異或 (XOR /
⊕) 這是不進位的二進制加法。請看加法表:0 + 0 = 0 ⊕ 0 = 00 + 1 = 0 ⊕ 1 = 11 + 0 = 1 ⊕ 0 = 11 + 1 = 1 ⊕ 1 = 0<-- 這是最關鍵的區別!
- 減法 (-) 也 是 異或 (XOR /
⊕) 因為1 + 1 = 0,所以1的加法反元素是它自己。因此,減去一個數等於加上同一個數。a - b就等於a + b,也就是a ⊕ b。 - 乘法 (×) 就是 與 (AND /
&) 這和我們熟悉的規則沒有區別:0 × 0 = 00 × 1 = 01 × 0 = 01 × 1 = 1
核心:在GF(2)域中,任何乘以2(或任何偶數)的項都會變成0。例如,2x 實際上是 (1+1)x=0⋅x=0 。
- 加法 (+) 就是 異或 (XOR /
在实数域(这里AI好像是被我带偏了)中
于是上面的
这个多项式还比较短,可以一眼丁真。对于推广情形,请使用Cantor-Zassenhaus 演算法(或其他演算方法),以便在多项式时间内完成在有限域上的因式分解
注
我也不懂这是什么东西,请不要拷打我
如何计算多项式的阶
接下来我们来看看如何计算可约多项式的理论分裂状态数目
首先先来讲一下不可约多项式
这是最简单、最清晰的情况。对于一个 n 次的不可约多项式
- 它所生成的所有非零循环的长度都是相同的。这个长度被称为该多项式的阶 (Order),记作 e。
- 分裂出的非零循环总个数可以通过一个非常简单的公式计算:
之前测试V2流密码生成器时最终使用的多项式序列为 0b1010 0000 0001 0001,即$$
x^{16} + x^{14} + x^{5} + x^
- 结论:它将所有65535个非零状态构成一个巨大的循环。这与实验结果完全吻合。
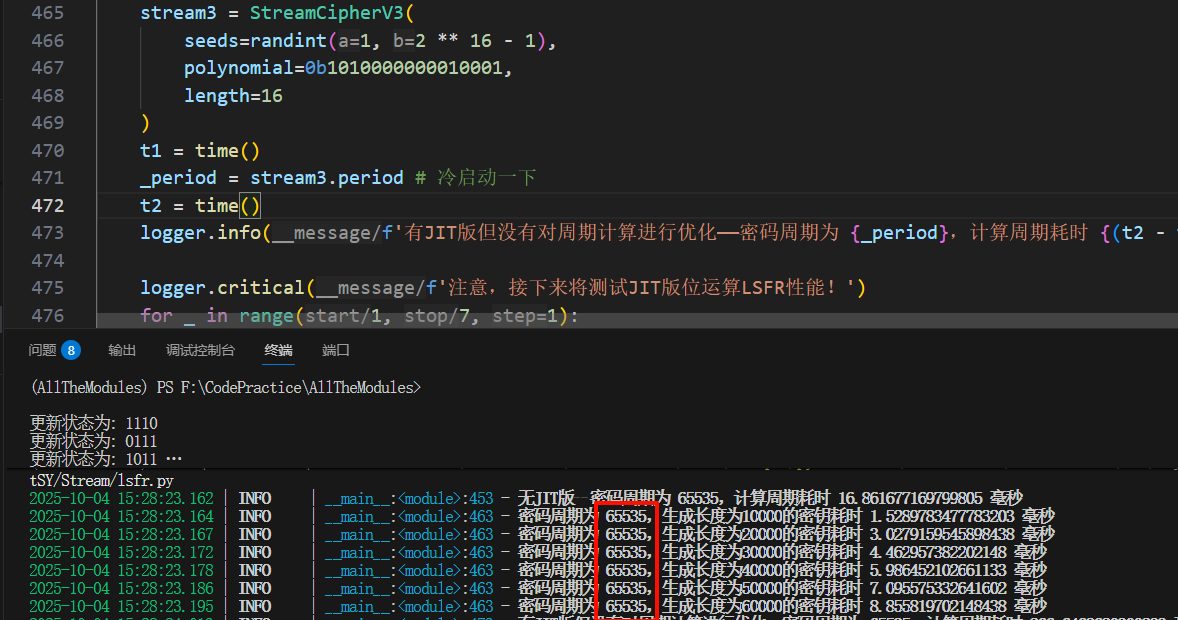
当多项式是可约的,情况就变得复杂得多,但依然有数学规律可循。
- 第一步:因式分解
需要先将可约多项式 - 第二步:计算各因子的阶 对每个不可约因子
- 第三步:计算循环结构 这里的公式比较复杂,它需要用到数论中的欧拉函数 (Euler's Totient Function,
一个简化的结论是:- LFSR产生的循环长度只可能是
- 循环的总个数与每个因子的次数
- LFSR产生的循环长度只可能是
让我们回顾 0b1010 的例子
- 多项式:
n=4。 - 数学分析 (简化版):因为因子是
x和x+1,它们的阶都是1。重复因子(x+1)²会引入长度为 1⋅2=2 的周期。最终的循环长度会是 - 程序化系统搜索结果:
- 1 个长度为 1 的循环 (零状态) (程序运行时懒得处理全零状态了,于是直接忽略了)
- 2 个长度为 6 的循环
- 1 个长度为 3 的循环
- 总循环个数 = 1 + 2 + 1 = 4 个
总结如下: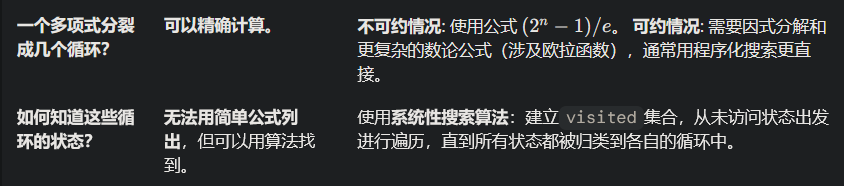
LCM是什么
LCM即Least Common Multiple,最小公倍数
LCM 在分析由可约多项式驱动的LFSR行为时,是计算其最终周期的核心数学工具
把LFSR看作一个由多个“小齿轮”组成的复杂钟表:
- 因式分解 = 拆解钟表 当我们对一个可约多项式
- 阶 (Order) = 小齿轮的齿数 我们已经知道,每一个不可约的“零件”
- LCM = 所有齿轮同时归位的时间 整个LFSR的完整状态,是由所有这些虚拟“子系统”的状态组合而成的。整个系统的状态要回到初始状态,就必须满足一个条件:所有的小齿轮必须同时回到它们的初始位置。
这个“同时归位”的最短时间点,正是所有齿轮齿数(即所有阶
所以,LCM 在流密码分析中的作用就是:
通过计算LFSR各个“子系统”周期的最小公倍数,来确定整个系统状态回归原点所需的最大周期长度。
假设我们有一个7位的LFSR,其多项式 P(x) 是可约的,分解后得到两个不可约因子:
那么,由这个7位LFSR产生的密钥流,其周期 T 是多少?
因为 7 和 15 互质,所以它们的最小公倍数是 7×15=105。
结论:这个7位LFSR产生的密钥流会每隔 105 位重复一次。
倒数定理该如何理解?
“倒数定理”是成立的,但它的应用比“把字符串倒过来”要微妙一些。
当我们为16位的LFSR选择一个多项式时,实际上是在定义一个16次的特征多项式 (Characteristic Polynomial)。
代码中
length=16显式指定了LFSR的长度,也隐含了特征多项式的最高次项是程序所传入的
polynomial整数(掩码)0b1010000000010001代表了多项式的其余部分。这个掩码对应的是:因此那个能产生65535周期的、完整的本原多项式实际上是:
倒数定理说的是,上面这个 16次的 C(x) 的倒数多项式
一个
重新排列一下:
倒数定理保证了上面这个 C∗(x) 也是一个16次的本原多项式。
而前面大端序对多项式的字符串形式反转,实际上并不是计算数学上的倒数多项式,
- 我们拿来的是代表
1010000000010001。 - 将这个字符串反转,得到了
1000100000000101。 - 这个新的掩码对应的多项式是 $$P_{mask}′(x)=x{15}+x+x^{2}+1$$
- 当我们用这个新掩码去测试时,我们实际上是在测试一个新的特征多项式:
现在对比一下:
- 数学上真正的倒数:
- 我们通过反转掩码得到的:
这两个多项式完全不同!
倒数定理保证了 C∗(x) 是本原的,但它并不保证我们通过反转掩码字符串得到的那个新多项式 C′(x) 也是本原的。 实验结果(它不是本原的)是正确的,恰好证明了“反转掩码字符串”这个操作与“求倒数多项式”在数学上是两回事。
这有点像在说“一个数字的倒数”。数字12的倒数是1/12。但如果我们只看它的个位数2,然后把2这个字符翻转过来(比如镜面翻转成5),得到的新数字5与1/12毫无关系。
我们反转的是“零件”(掩码),而定理说的是“整体”(完整的特征多项式)的属性。
LSFR位宽与多项式次数的联系
所以,为什么不减一呢?
这便是接下来需要辨析的程序中的“多项式掩码”和数学上的“特征多项式”之间的关系。
在整个LFSR的模拟中,我们实际上在和两个不同层面的“多项式”打交道:
- 数学上的“特征多项式” (Characteristic Polynomial)
- 这是我们在论文或教科书中看到的完整形式,例如 $$C(x)=x{16}+x+x{13}+x+1$$
- 它的次数是 16次。
- 它的二进制表示需要 17位 (
0b11010000000100011,如果完整表示的话)。(在已经删除的文案中,用于演示的代码所使用的多项式正是掩码,而非特征多项式) - 对于这个特征多项式,我们此前的结论(给StreamCipherV2打补丁时;StreamCipherV2不是FiLSFRV2)
LFSR长度 = 它的位宽 - 1是完全正确的。
- 程序中的“反馈掩码” (Feedback Mask)
- 这是我们代码中的
self.polynomial变量。 - 它的作用是什么?是与一个与之等位宽(在这里是16位)的状态
self.seeds进行&运算。 - 因此,这个掩码本身有意义的部分也只有 16位。它实际上只代表了特征多项式中,除了最高次项
- 对于上面的例子,它在代码中对应的
polynomial掩码就是0b1010000000010001。 - 这个掩码的
bit_length()是 16。
- 这是我们代码中的
注意
写到这里的时候,在程序实现中,LSFR长度就是多项式长度——这个实现是错误的,但是我当时没写单元测试,所以没发现这个问题
所以……下面的分析其实是错误的……
现在,关键点来了:
(最新的)程序推断LFSR长度时,使用的依据是程序中的“反馈掩码”,而不是数学上的“特征多项式”。
- 对于一个 n 位的LFSR,其反馈掩码的位宽最大就是 n
- 因此,没有指定
length时,通过polynomial.bit_length()来获取掩码的位宽,并以此作为LFSR的长度n,是一个非常合理且正确的工程推断
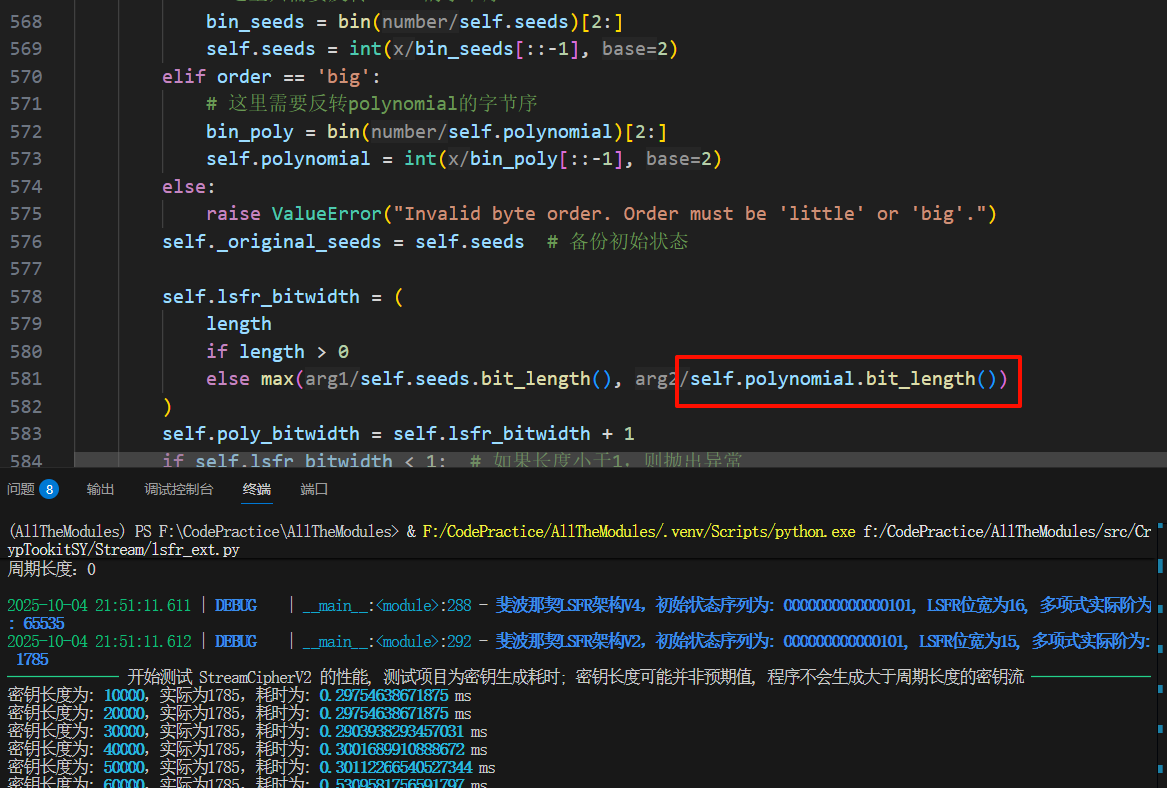
现在我们就能解释为什么V4正确而V2错误了:
- V4 的逻辑 (正确):
self.lsfr_bitwidth = ... else max(self.seeds.bit_length(), self.polynomial.bit_length())- 当传入
polynomial=0b1010000000010001时,polynomial.bit_length()是16。 max(...)正确地将lsfr_bitwidth设置为 16。- 结果:一个16位的LFSR配上一个16位的有效掩码,完美匹配,周期为65535。
- 当传入
- V2 的逻辑 (错误):
# 打的补丁就是这个多项式长度-1 self.lsfr_bitwidth = ... else (polynomial.bit_length() - 1)- 当传入同一个
polynomial时,polynomial.bit_length()是16。 16 - 1导致lsfr_bitwidth被错误地设置为了 15。- 结果:一个15位的LFSR配上一个16位的掩码,尺寸错配,数学结构被破坏,周期为
1785。
- 当传入同一个
因此“为什么不是多项式长度减1”的答案是:
因为我们在代码中用来推断的“多项式长度”,是“反馈掩码”的位宽,而不是“特征多项式”的位宽。对于一个n位的LFSR,其掩码的合理位宽就是n,因此直接使用
polynomial.bit_length()是正确的。
而之前的V2补丁之所以出错,是因为它错误地将适用于“特征多项式”的 位宽-1 规则,用在了“反馈掩码”上。而V4(以及AI给的V3)所采用的多项式位宽等同于LSFR长度 逻辑,则正确地处理了程序实现层面的变量关系。
别急,还有反转!
LSFR位宽之谜(二)
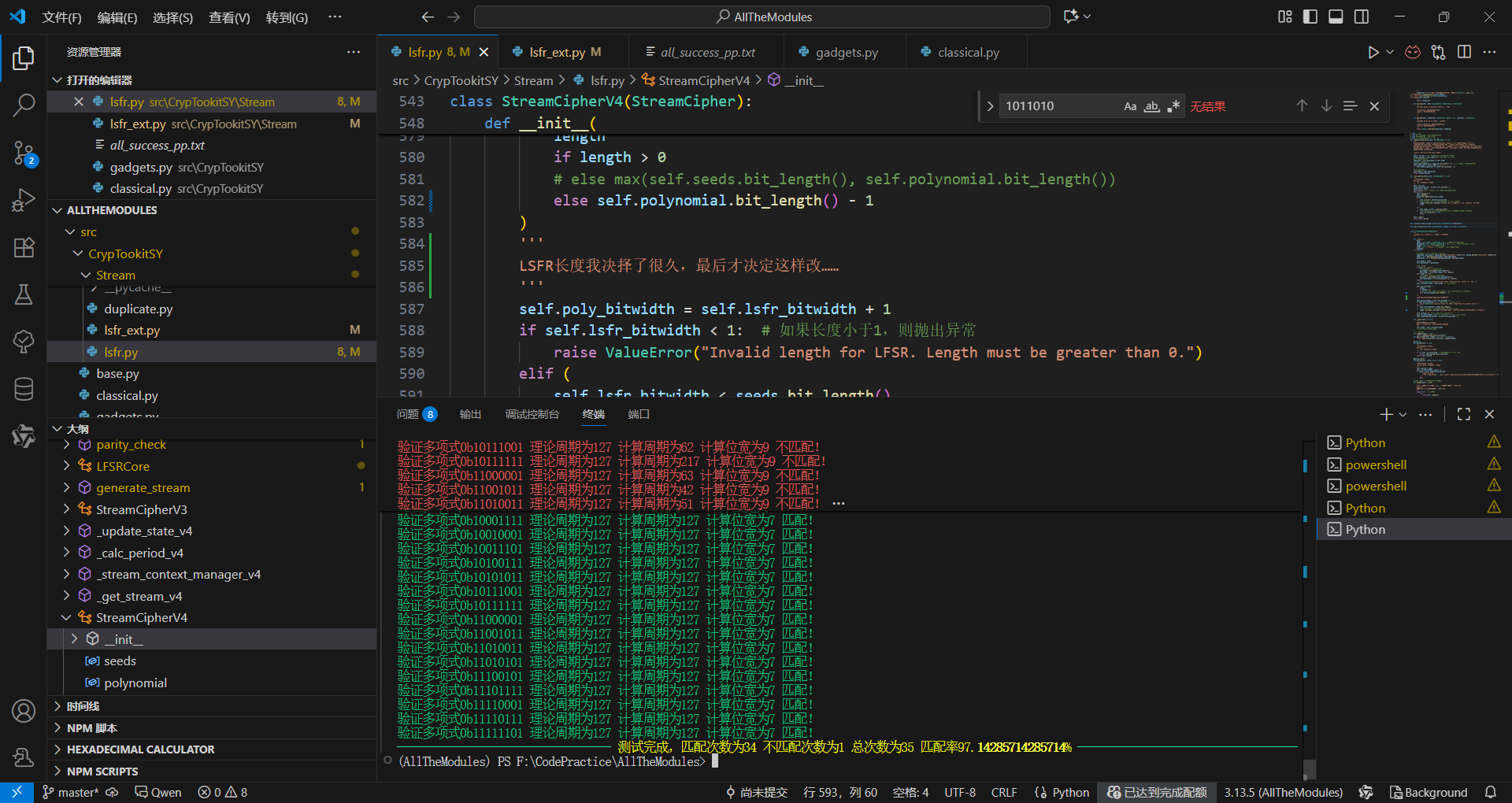
改回多项式长度-1时单元测试符合预期,但是标准周期计算又炸了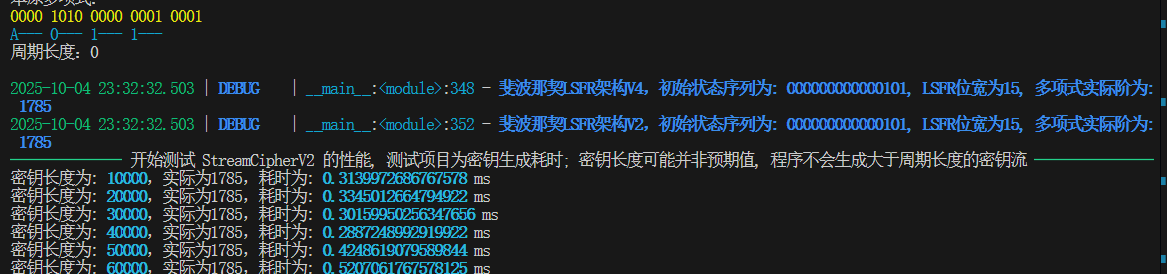
我真是服了呀
def _update_state_v4(sc_inst: StreamCipher) -> int:
self = sc_inst # 改一下变量命名,以兼容提取出的代码
output_key_bit = self.seeds & 1 # 取出最低位作为输出
# 计算新的状态比特
temp_bits = self.polynomial & self.seeds
# 然后进行奇偶校验
next_state_single_bit = temp_bits.bit_count() % 2 # 用于构成下一个状态的新比特
next_state_bits = (self.seeds >> 1) | (
next_state_single_bit << (self.lsfr_bitwidth - 1)
)
# 更新状态比特
self.seeds = next_state_bits
return output_key_bit
妈的可算是改完了
不同类型的LSFR
線性反饋移位暫存器(LFSR)主要有兩種經典的架構或「類型」:
- 斐波那契LFSR (Fibonacci LFSR)
- 伽羅瓦LFSR (Galois LFSR)
教材上主要是前者
斐波那契LSFR的核心思想是外部反馈,可以將其工作模式理解為「先計算,再注入」
工作流程比喻 (傳送帶模型):
- 檢查 (Inspect):在傳送帶(暫存器)移動前,幾個預設的感測器(抽頭)會讀取對應位置上物品的狀態(0或1)。
- 計算 (Calculate):所有感測器的讀數被送到一個外部的中央計算器(XOR邏輯),計算出一個新的物品狀態。
- 移位 (Shift):傳送帶整體移動一格,最末端的物品掉出(成為輸出位)。
- 注入 (Inject):剛剛計算出的新物品被放到傳送帶空出來的最前端。
伽罗瓦LFSR也能產生完全相同的最大長度序列,但它的工作方式非常不同
- 核心思想: 內部反饋 (Internal Feedback)。
- 可以將其工作模式理解為「先移位,再(有條件地)異或」。
- 工作流程比喻 (內部聯動模型):
- 移位和輸出 (Shift & Output):傳送帶首先整體移動一格,最末端的物品掉出(成為輸出位)。最前端空出一個位置,並總是先放上一個
0。 - 內部聯動 (Internal Feedback):檢查剛剛掉出去的那個物品。
- 如果掉出去的是
1:那麼傳送帶上所有“抽頭”位置的物品,會就地與1進行一次異或(即狀態翻轉,0變1,1變0)。 - 如果掉出去的是
0:則什麼也不發生。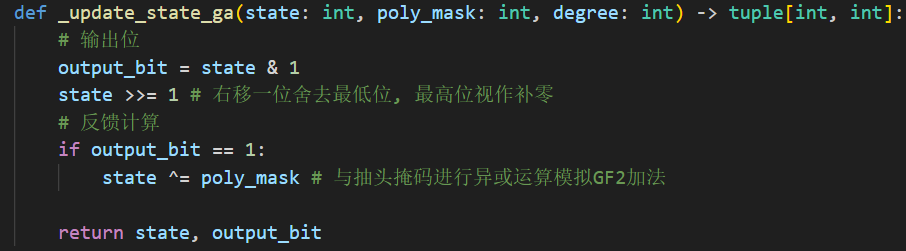
- 如果掉出去的是
- 移位和輸出 (Shift & Output):傳送帶首先整體移動一格,最末端的物品掉出(成為輸出位)。最前端空出一個位置,並總是先放上一個

一些重要结论如下:
- 數學等價性: 對於同一個n次本原多項式,斐波那契LFSR和伽羅瓦LFSR(使用其倒數多項式)產生的序列內容是完全相同的(都是m序列),僅僅是相位不同(即序列的起始點錯開了幾位)。
- 性能差異: 在硬體和軟體實現中,伽羅瓦結構通常被認為具有輕微的性能優勢。
LSFR与多项式类型不匹配时会发生什么
根据维基百科所述,LSFR基础核心结构只有斐波那契LSFR和伽罗瓦LSFR两种,其他更复杂的LSFR都是由这两种结构组合而来的
相对的,基础的本原多项式也有两种,分别对应斐波那契LSFR(以下简称F)和伽罗瓦LSFR(以下简称GF)。两者在密码学上是等价的,对于同一个
若把一個n位的LFSR看作一個向量,则每一次的 _update 操作,都可以用一個T 來表示
這意味著,LFSR產生的整個狀態序列,就是初始狀態向量在矩陣 T 的不斷乘以作用下的結果:
多項式 T 的特征多项式 (Characteristic Polynomial)。多項式的數學屬性(如是否本原)直接決定了矩陣 T 的屬性(如其循環長度)
现在,對於同一個數學多項式
- 斐波那契LFSR:我們可以構建出一個與之對應的狀態轉移矩陣,稱之為
- 伽羅瓦LFSR:我們也可以構建出它的狀態轉移矩陣
在線性代數中有一個基本定理:一個矩陣和它的轉置矩陣,擁有完全相同的特徵多項式。
這便是兩者的數學聯繫!
- 因為
- 如果
- 那麼,由
本原多项式的循环长度决定了理想情况下,F和GF型LSFR都能遍历全部状态,只是遍历路径可能不完全一致罢了: - 狀態序列 (State Sequence): 兩種LFSR遍歷所有狀態的順序不同。
- 輸出序列 (Output Sequence): 由於輸出位是從每個狀態中提取的,狀態的順序不同,導致輸出位的序列也不同。
- 相位差異 (Phase Difference): 易证得 ,這兩條不同的輸出序列,其中一條必定是另一條的循環移位 (cyclic shift)。也就是說,伽羅瓦產生的序列
...c, d, e, f...,一定可以在斐波那契產生的無限序列...a, b, c, d, e, f, g, h...中找到完全一樣的片段。它們本質上是同一首歌,只是從不同的小節開始唱而已。
说完了理论,那么如何实操呢?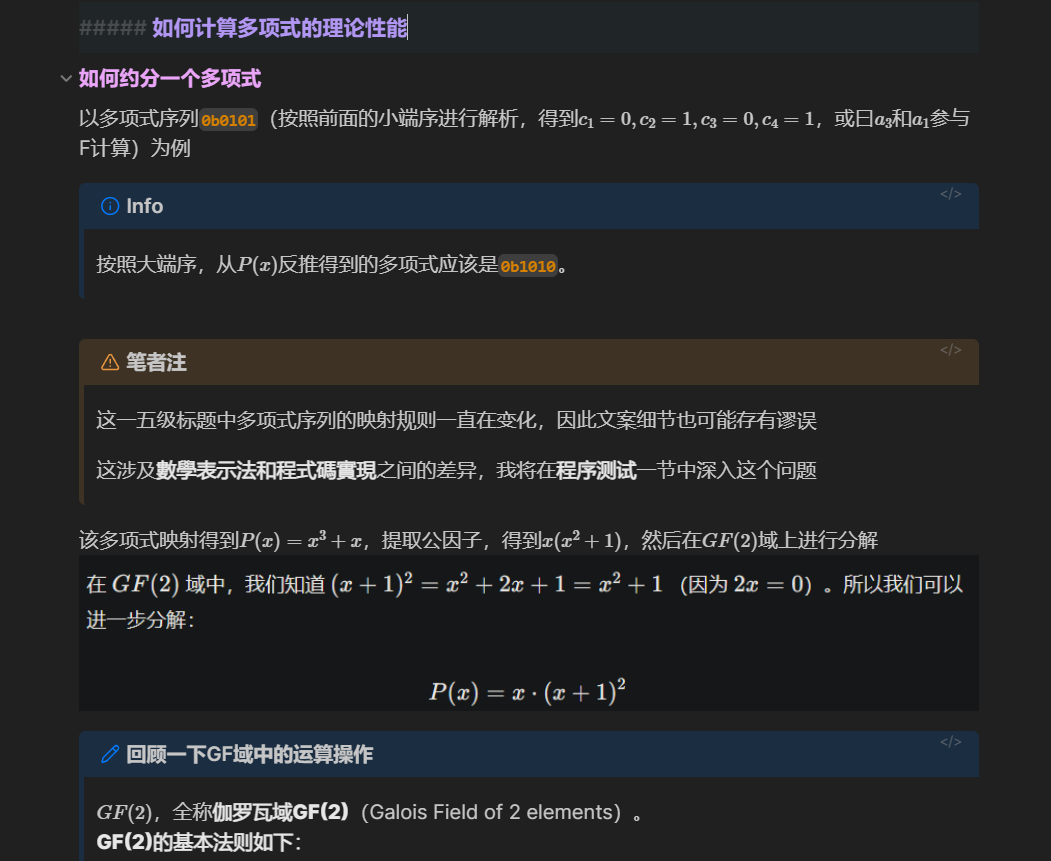
之前的小节中已经演示过如何计算倒数多项式,公式是$$P^*(x) =x^n P (\frac{1}{x})$$
而F与GF型LSFR的本原多项式正好互为倒数
那么,应该如何将这一过程变成程序代码呢?
如何程序化多项式倒数计算
我们的目标是证明:“求倒数多项式”在数学上的操作,等价于“将多项式的整数表示进行比特反转”
首先选择一个具体的例子,比如一个4次本原多项式——
之前已经(左脑反驳右脑地写代码)推导过n次本原多项式需要n+1比特位宽来表示,那么这里的0b10011
接下来计算
然后乘上
转回二进制表示为:0b11001
现在我们来比较原始多项式和倒数多项式的二进制表示:
- 原始多项式
- 完整形式: $$P(x) = 1 \cdot x^4 + 0 \cdot x^3 + 0 \cdot x^2 + 1 \cdot x^1 + 1 \cdot x^0$$
- 系数序列:
(1, 0, 0, 1, 1) - 二进制表示:
10011
- 倒数多项式 P∗(x)=x4+x3+1
- 完整形式: $$P(x) = 1 \cdot x^4 + 1 \cdot x^3 + 0 \cdot x^2 + 0 \cdot x^1 + 1 \cdot x^0$$
- 系数序列:
(1, 1, 0, 0, 1) - 二进制表示:
11001
显然,11001正是10011的完全反转!
这个规律并非巧合。让我们看看一个通用的项
- 在
- 代入
- 乘以
这意味着,原始多项式中k变成了n-k。
对于一个长度为n+1的比特序列(索引从0到n),将索引k的比特移动到索引n-k的位置,这正是比特反转操作的定义!
流密码:薄弱在哪里
主要弱点:线性
这是单个或多个的LFSR线性组合的最根本、最致命的缺陷,也是所有其他问题的根源。- 薄弱點描述:
LFSR的整个行为可以用一组简单的线性方程来描述。具体来说,输出密钥流的每一位,都是其内部状态各位元的线性组合(即异或和)。 - 后果:
这种线性关系使得整个序列变得可预测。攻击者不需要猜测您的初始种子,他们可以通过代数方法直接“解方程”,反推出LFSR的结构。 - 对应的攻击技术: Berlekamp-Massey 算法
- 这是针对所有线性序列的“银色子弹”。
- 攻击原理: 只要攻击者能截获一小段连续的密钥流(对于一个n位的LFSR,理论上只需要 2n 位的密钥流),这个算法就能在极短的时间内,高效地计算出这个LFSR的反馈多项式
- 攻击效果: 一旦多项式被反推出来,攻击者就拥有了和您完全一样的密钥流生成器。他可以同步地生成过去和未来的所有密钥流,您的加密瞬间被完全破解。
- 薄弱點描述:
使用模式弱点:密钥流复用 (Keystream Reuse)
这个弱点是所有(不带认证的)流密码的通病,但在简单的LFSR上体现得尤为直接。- 薄弱點描述:
使用完全相同的密钥流(即相同的种子和多项式)去加密两条或多条不同的明文。这种情况被称为“两次使用一密 (Two-Time Pad)”。 - 后果:
攻击者可以将两段密文进行异或,从而完全消除密钥流,直接得到两段明文的异或结果。 - 对应的攻击技术: 统计分析 与 密文对比攻击 (Crib-Dragging)
- 攻击原理: 攻击者拿到了 P1⊕P2。如果他们能猜到其中一段明文的一部分(例如,文件头
"HTTP/"、英文常用词" the "),他们就可以通过这个已知的“小抄 (crib)”去滑动比对,逐步还原出另一段明文的内容。 - 攻击效果: 即使不知道密钥,攻击者也能在很大程度上恢复出两条明文的内容。
- 攻击原理: 攻击者拿到了 P1⊕P2。如果他们能猜到其中一段明文的一部分(例如,文件头
- 薄弱點描述:
结构性弱点:延展性 (Malleability)
您的LFSR流密码只提供了保密性,完全没有提供完整性 (Integrity) 保护。- 薄弱點描述:
由于加密就是简单的逐位异或,攻击者可以在不知道明文内容的情况下,对密文进行可预测的篡改。 - 后果:
攻击者可以精确地翻转密文中的某个位元,从而导致解密后的明文中对应的位元也被翻转。
Pdecr′=Cenc′⊕K=(Cenc⊕1)⊕K=(Penc⊕K⊕1)⊕K=Penc⊕1 - 对应的攻击技术: 比特翻转攻击 (Bit-Flipping Attack)
- 攻击原理: 攻击者拦截了一段密文,虽然他看不懂,但他知道其中某几位可能对应着关键信息(例如,转账金额、指令代码)。他只需将密文中的这几位进行翻转(
C_i = C_i \oplus 1),接收方在解密后,对应的明文位也会被翻转。 - 攻击效果: 攻击者可以随心所欲地篡改传输的消息内容,造成严重后果(例如,将“转账给Alice 100元”改成“转账给Eve 900元”)。
- 攻击原理: 攻击者拦截了一段密文,虽然他看不懂,但他知道其中某几位可能对应着关键信息(例如,转账金额、指令代码)。他只需将密文中的这几位进行翻转(
- 薄弱點描述:
配置性弱点:周期过短 (Short Period)
你猜猜为什么文案里的代码演示从V2、V3到V4,一直到现在的FiLSFR,始终在重构
- 薄弱點描述:
错误地选用了一个非本原或可约的多项式。 - 后果:
密钥流会在很短的时间内开始重复。一旦重复,其后续所有序列都变得完全可知。 - 对应的攻击技术: 频率分析 / 统计攻击
- 攻击原理: 攻击者收集足够长的密文,通过分析其统计规律,可以发现密钥流的周期。一旦周期被确定,破解难度就大大降低。
- 攻击效果: 相当于将一个长密钥问题,降级成了一个短密钥问题。
针对线性LSFR的
代码实现
def simple_bm_attack():
# --- 1. 生成目标密钥流序列 ---
# 使用一个已知的3次本原多项式 x³ + x + 1 (0b1011)
sc = FibornacciLSFRCore(seed=0b1, polynomial=0b1011)
# 根据Berlekamp-Massey算法,需要 2*L 的序列长度
# L 是LFSR的真实长度,这里是 sc._degree = 3
max_length = sc._degree * 2
sc_key_gen = sc.keys(max_length) # 假设 keys() 返回生成器
keys = list(sc_key_gen)
print(f"目标LFSR长度 L=3, 多项式 C(x)=x³+x+1")
print(f"截获的 2L={max_length} 位密钥流: {keys}")
# --- 2. Berlekamp-Massey 算法初始化 ---
# 跳过开头的0 (在这个例子中没有)
key_idx = 0
while key_idx < len(keys) and keys[key_idx] == 0:
key_idx += 1
if key_idx == len(keys):
print("序列全为0,无法分析。")
return
# C(x) - 当前的连接多项式
Cx = {key_idx + 1, 0}
# L - 当前的LFSR长度
curr_length = key_idx + 1
# B(x) - “仓库”里上一个版本的连接多项式
Bx = {0}
# m - 上一次“大修正”时的时间点
m = key_idx
# b - 辅助变量,记录“延时”
b = 0
# --- 3. 主循环:迭代处理序列 ---
for n in range(key_idx + 1, max_length):
# n 是当前正在处理的位元的索引
# --- 步骤 1: 做出预测 ---
# 预测 s[n] 的值
prediction = 0
# 根据 C(x) = 1 + c₁x + c₂x²...
# 预测公式是: s[n] = c₁s[n-1] + c₂s[n-2] + ...
for i in Cx:
if i != 0: # x⁰=1 项不参与抽头
prediction ^= keys[n - i]
# --- 步骤 2: 计算差异 (Discrepancy) ---
# 差异 d = 真实值 ⊕ 预测值
discrepancy = keys[n] ^ prediction
# --- 步骤 3: 根据差异决定是否修正 ---
if discrepancy == 1: # 预测错误!需要修正
# 拷贝一份 C(x) 以备后用
Cx_old = Cx.copy()
# --- 核心修正公式 ---
# C_new(x) = C(x) + B(x) * x^(n-m)
# 集合表示: Cx_new = Cx ^ {item + n - m for item in Bx}
delay = n - m
correction_term = {item + delay for item in Bx}
Cx ^= correction_term # 利用set的对称差集运算模拟GF2上的加法
# --- 步骤 4: 判断是否需要增加LFSR长度 L ---
if curr_length <= n / 2:
# 是时候进行“大修正”了
# 更新 L
curr_length = n + 1 - curr_length
# 更新“仓库”和“时间点”
m = n
Bx = Cx_old
# --- 4. 攻击结束,输出结果 ---
# 为了与您的LFSR实现约定一致,我们找到的多项式是P(x)
# 特征多项式 C(x) = 1 + P(x)
# 所以 P(x) = C(x) - 1,即从集合中去掉0
# Cx.discard(0)
# 不要去掉, 这一项可以用于判断多项式次数
# 将集合 {2, 3} 转换为整数 0b1011
reconstructed_poly = 0
for i in Cx:
reconstructed_poly |= (1 << i)
reconstructed_poly |= (1 << curr_length) # 加上最高位的 x^L 项
print(f"\n攻击完成:")
print(f'反推得到的连接多项式 C(x) (次幂集合): {Cx}')
print(f'反推得到的LFSR长度 L: {curr_length}')
print(f'重构出的特征多项式 (整数): {bin(reconstructed_poly)}')
rev_reconstructed_poly = reverse_polynomial(reconstructed_poly, curr_length)
print(f'重构出的特征多项式倒数 (整数): {bin(rev_reconstructed_poly)}')提示
Gemini写的,我反正没看懂
算法原理 && 算法步骤
BM演算法要解决的核心是:
给定一个(时序敏感)二进制序列
「找到最短的LFSR」等價於找到兩樣東西:
- 最短的長度 L: 我們稱之為序列的线性复杂度 (Linear Complexity)。
- 對應的特征多项式 C(x): 這個多項式定義了LFSR的反馈逻辑。
演算法維護幾個關鍵變數,並在讀取序列的第 k 個位元時進行更新:
C(x): 當前猜測的連接多項式。L: 當前猜測的LFSR長度。
对于一个长度为 L 的 LFSR,其特征多项式为
在 GF(2)(二进制域)中,加法就是异或(XOR),所以上式变为:$$s_n = s_{n-1} & c_1 ⊕ s_{n-2} & c_2 ⊕ ... ⊕ s_{n-L} & c_L$$
(这里 & 是逻辑与,⊕ 是异或。m: 上一次更新L時,我們讀到了第幾個位元。B(x): 上一次更新L時,舊的C(x)是什麼樣的。
在處理第 k 個位元 sk 時,演算法執行以下四步:
第一步:計算“差異” (Discrepancy) 演算法用當前的LFSR模型(由
L和C(x)定義)來計算一個“預測值”。然後,計算這個預測值與真實值 sk 之間的差異d。在GF(2)域中,這個差異就是異或:- 如果
d = 0,預測正確。 - 如果
d = 1,預測錯誤。
而在最开始,我们什么都不知道,就做一个最简单的猜测:这个序列是全零序列,由一个长度为0的LFSR生成。此时
接下来算法逐个读取序列中的比特- 如果
第二步:如果預測正確 (d = 0) 什麼都不用做。當前的LFSR模型仍然可以解釋到目前為止的所有序列。繼續處理下一個位元。
第三步:如果預測錯誤 (d = 1) 這一步是演算法的精髓。我們需要更新我們的多項式
C(x)來修正這個錯誤。BM演算法的絕妙之處在於,它使用上一次犯錯時的狀態來幫助修正這一次的錯誤。新的多項式
- 直觀解釋:
C(x)是我們當前這個“不完美”的模型。B(x)是我們“倉庫”裡存著的、上一個被證明不夠用的舊模型。x^{k-m}是一個“延遲”項,它將舊模型B(x)的影響“平移”到當前這個出錯的時間點k上。- 通過將當前模型與這個“經過延遲修正的舊模型”進行異或,我們神奇地得到了一個既能解釋過去所有序列、又能修正當前這個錯誤的新模型。
- 直觀解釋:
第四步:是否需要增加LFSR的長度 (L)? 在修正了多項式之後,演算法還需要決定是否要增加LFSR的長度
L。規則是:
如果當前模型的“好日子”(即連續預測正確的步數)已經過得太久,具體來說是超過了其自身長度的一半,那麼這次的修正就需要一個更長的LFSR才能容納。數學上的判斷條件是
- 如果需要增加長度:
- 更新長度:
- 更新“記憶”: 由於我們剛剛進行了一次“重大升級”(增加了L),我們需要更新我們的“倉庫”,為下一次可能的重大升級做準備。
- 將當前這個不完美的
C(x)存入B(x)。 - 記錄下當前的時間點
k到m。
- 將當前這個不完美的
- 更新長度:
- 如果不需要增加長度: 則保持
L和“倉庫”裡的B(x),m不變。
- 如果需要增加長度:
演算法不斷重複這四步,直到讀完所有給定的序列位元。最終得到的 L 和 C(x),就是能夠生成該序列的最短LFSR的長度和連接多項式。
算法推导
101 -> 110 | 1
110 -> 111 | 0
111 -> 011 | 1
011 -> 001 | 1
001 -> 100 | 1
100 -> 010 | 0
010 -> 101 | 0
FiLSFRDebug: 当前状态[101] 状态转移多项式[1 + x] 特征多项式[1011] 掩码多项式[011] 理论周期[2^3-1=7] 计算周期[7]对于一个长度为
展开后得到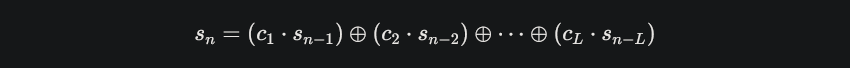
n位。L位。0或1),它们就是LFSR的“基因”,定义了反馈逻辑。
这组系数正是连接多项式(或称状态转移多项式)
BM算法并非要 建立一个巨大的方程组然后去求解,而是采用一种迭代的、动态的方式来“逼近”正确的系数 cᵢ
小总结
线性 (可被代数方法破解)
⬇️
Berlekamp-Massey算法 (核心攻击)
流式异或 (无状态、无认证)
⬇️
金鑰流重用 (使用模式漏洞)
比特翻转攻击 (篡改漏洞)
多项式选择 (配置问题)
⬇️
週期过短 (可被统计分析破解)
流密码:非线性输出
多个LSFR的线性组合
最初,人们发现一个使用本原多项式的LFSR能产生周期极长(m序列)、统计特性又非常接近随机噪声的序列。这看起来是完美的密钥流来源。但Linear FSR最致命的弱点便是线性
而Berlekamp-Massey (BM) 算法的出现,宣告了单一LFSR作为密码的死刑。该算法可以在获得仅仅2n位的输出序列后,就完全反推出这个n位LFSR的结构,从而生成全部的密钥流。
非线性输出
密码学家们最终意识到,唯一的出路就是必须在从LFSR内部状态到最终输出位的路径上,插入一个非线性的“屏障”。
流密码中的非线性输出本质上是一种布尔函数,它接收来自LSFR内部的多个输入位元,并输出一个单一的位元,并输出一个单一的位元
一个函数,如果可以表示为简单的异或和(GF2域上的加法),如
任何布尔函数都可以写成代数正规式ANF(标准形式),即所有输入数的乘积的异或和。一个函数的代数次数就是其Algebraic Normal Form中乘积项包含的变量最多的那一项的个数
- 线性函数:代数次数为1
- 非线性函数:代数次数大于1
而在实际的流密码设计中,并非任何非线性函数都是好的。一个密码学上良好 的非线性函数,除了要具备高非线性度,还需要有良好的平衡性、抗相关性等特性。以下是主要的实现方式 :
- 非线性滤波器生成器 (Non-linear Filter Generator)
- 设计思想:这是《观察器攻击》论文中涉及的模型 。它只使用一个(通常很长的)LFSR。但输出不再是简单地取某一位,而是从LFSR的内部状态中抽取多个位 (
- 如何破坏线性: 最终的输出
g是非线性的(例如包含与门AND,即乘法项),z(k)和内部状态x(k)之间的关系不再是简单的线性方程,BM算法因此失效。
- 设计思想:这是《观察器攻击》论文中涉及的模型 。它只使用一个(通常很长的)LFSR。但输出不再是简单地取某一位,而是从LFSR的内部状态中抽取多个位 (
- 非线性组合生成器 (Non-linear Combiner)
- 设计思想:这是第二阶段“线性组合”的进化版。它同样是并行运行多个LFSR,但不再是将它们的输出简单异或,而是同样将这些输出位 (x1,x2,x3,…) 送入一个非线性布尔函数
g(…),由g产生最终输出。 - 如何破坏线性: 同样,
z(k) = g(x₁(k), x₂(k), ...)这个关系是非线性的,从而使BM算法失效。
- 设计思想:这是第二阶段“线性组合”的进化版。它同样是并行运行多个LFSR,但不再是将它们的输出简单异或,而是同样将这些输出位 (x1,x2,x3,…) 送入一个非线性布尔函数
- S盒
- 结构: S盒在塊密碼(如AES)中更為常見,但它在流密碼中也可以作為一個強大的非線性組件。您可以將一個S盒理解為一個預先計算好的、複雜的非線性函數的“查找表”。
- 工作方式: 從LFSR的內部狀態中取出若干位元(例如8位),將這8位元組成的數字作為地址,去S盒這個大表格中查找對應的輸出值。這個查找過程本身就是一個高度非線性的映射。
- 例子: 一些流密碼設計會將LFSR的輸出或其他內部狀態位元送入一個小型S盒(例如4位輸入4位輸出),以產生高度混淆的輸出。
无论是采用“滤波”还是“组合”乃至密钥代换盒的方式,现代设计的核心都是一样的:利用LFSR作为高速、长周期的“随机性引擎”,然后用一个精心设计的非线性“混淆层”g(x)来彻底掩盖其线性的内在结构。
攻击者现在面对的,不再是一个可以用BM算法解决的线性方程组,而是一个求解非线性多元方程组的难题。正如论文中提到的,这通常是NP问题,计算复杂度呈指数级增长,从而保证了密码的安全性 。
程序实现
三输入多数表决函数(三变量表决器)
三输入多数表决函数也即三变量表决器(亦称多数逻辑门 或 表决电路)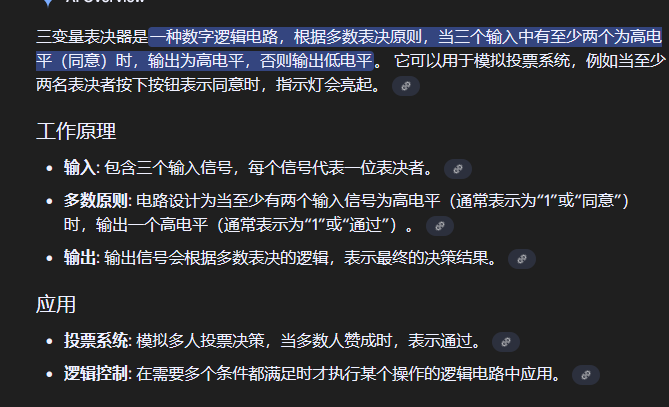
一个三输入的多数决函数/三变量表决器,其核心功能是:当输入的三个比特位中,有半数以上(即两个或三个)为 1 时,输出就为 1;否则,输出为 0。
根据真值表写出的输出公式如下
(A · B):当A和B都是1时,结果为1。(A · C):当A和C都是1时,结果为1。(B · C):当B和C都是1时,结果为1。 将这三种“至少有两个是1”的情况异或起来,就构成了完整的多数决逻辑
这个函数的代数表达式中包含了多个乘法项(AND/与运算)。正是这些乘法项的存在,使得多数决函数成为了一个非线性函数(其代数次数为2)
忠实的实现如上
取巧的实现如下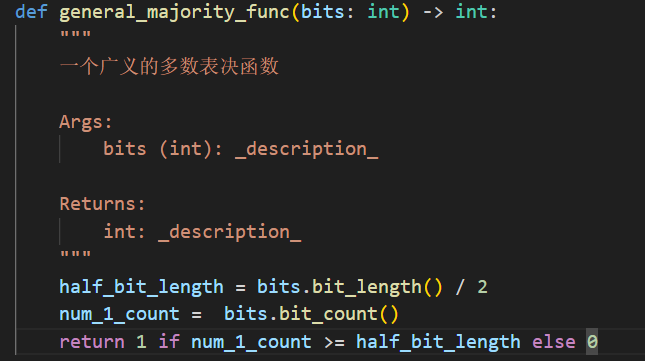
既然都是多数表决,那我直接抽比特出来看不就好了?
class FiFSR(FibornacciLSFRCore):
"""
添加了随机化密钥输出的斐波那契FSR计算类
这一代是为了测试观察器攻击的, 考虑到性能问题, 在多项式阶数比较大(大于12)的时候将关闭周期自动计算
Params:
randomize: (bool = True) 随机密钥比特输出, 默认为True
taps: list[int] 抽头序列
"""
def __init__(self, taps: list[int], randomize: bool = True, **kwargs) -> None:
self._taps = taps
if len(taps) < 1:
logger.error("抽头序列不可为空, 已自动将randomize设置为False, 启用线性循环密钥比特输出")
randomize = False
if len(taps) < 3:
logger.error("抽头序列至少应为三位位宽")
super().__init__(randomize=randomize, **kwargs)
if self._degree > 12: # 斐波那契FSR的周期自动计算功能
self._is_calculated = True # 通过将这一属性设为True来关闭周期自动计算
def _non_linear_output(self) -> int:
"""
非线性输出
"""
tapped_bits = [
self._state >> tap & 1 for tap in self._taps
]
return general_majority_func(tapped_bits)
def _update_state(self) -> int:
"""
更新状态序列
"""
output_bit = super()._update_state() # 仍然需要更新状态
if self._randomize:
return self._non_linear_output() # 向前兼容, 所以update_state仍然必须返回输出比特
return output_bit
if __name__ == '__main__':
# x^21 + x^13 + x^5 + x^2 + 1
# 1 - 0000 - 0010 - 0000 - 0010 - 0101
# sc = FiFSR(seed=0b01, polynomial=0b1011, randomize=True, taps=[0, 1, 2])
sc = FiFSR(seed=0b011100101101, polynomial=0b100000001000000100101, randomize=True,
taps=[1, 7, 17]
# taps = [2, 5, 8, 13, 19]
)
print(sc)
byte_key_gen = sc._stream_n_bits()
keys = [padding_8_zeros(bin(next(byte_key_gen))[2:]) for _ in range(20)]
print(keys)不过有多数表决了是一回事,选择合适的抽头序列的话又是另一回事
选择抽头位置,实际上是在设计那个非线性布尔函数 g(x) 的输入。一个“好”的 g(x)(由其输入抽头决定)需要在以下几个关键的、有时甚至是相互冲突的密码学指标之间取得良好的平衡。
高非线性度 (High Non-linearity)
目标: 使输出函数
g(x)的行为尽可能地远离任何线性函数。为何重要: 这是抵抗线性攻击的基础。如果
g(x)可以被一个简单的线性函数很好地“近似”,攻击者就可以通过统计方法,建立一个关于LFSR内部状态的线性方程组并求解。如何选择抽头: 选择的抽头位组合在一起,通过非线性函数(如多数决),应能产生一个代数次数较高、难以被线性函数模拟的结果。
高相关免疫性 (High Correlation Immunity)
目标: 确保输出密钥流位元与任何一个单独的输入抽头位元(或一小部分抽头位元的组合)之间没有统计相关性。
为何重要: 这是抵抗相关攻击 (Correlation Attacks) 的关键。如果输出位与某一个内部状态位(例如
xᵢ)高度相关(例如,z(k)有70%的时间都等于xᵢ(k)),攻击者就可以忽略其他所有部分,专注于猜测这一个LFSR序列,从而将一个复杂的问题大大简化。如何选择抽头:
分散性 (Dispersion):抽头位置应该在LFSR的20位长度上尽可能地分散。避免选择相邻的位,例如
[0, 1, 2](您之前的实验),因为相邻的LFSR状态位之间本身就存在极强的线性关系(一个就是另一个的下一时刻),这会严重削弱相关免疫性。数量: 抽头的数量(即
g(x)的输入变量个数)也很重要。更多的输入通常有助于提高相关免疫性。
高代数免疫性 (High Algebraic Immunity)
目标: 确保不存在一个低次数的布尔函数
h(x),使得g(x)·h(x) = 0或(g(x)⊕1)·h(x) = 0成立。为何重要: 这是抵抗代数攻击 (Algebraic Attacks) 的核心。代数攻击会尝试建立一个描述整个系统的、低次的多元方程组。如果存在一个低次的“零化子 (annihilator)”函数
h(x),就会给攻击者提供额外的、简化的方程,从而大大降低求解的复杂度。如何选择抽头: 这与
g(x)函数本身的代数结构关系更密切,但选择“代数关系”更复杂的抽头位置有助于提升此项指标。
注
写(抄AI)到这里的时候已经是10号了,只能抓瞎硬上了
根据上面的原则,总结得到下面的规则(为多数决函数选择抽头 taps = [i, j, k]):
- 规则一:必须分散! 不要选择相邻(这时上一个抽头和下一个抽头的相位差不够大)或离得很近的位置。
- 规则二:避免简单的数学关系。 例如,不要选择
[2, 4, 8]这种成倍数关系的位置。 - 规则三:包含高位和低位。 最好能跨越整个LFSR的长度。
我们可以选择一个低位、一个中位、一个高位。 taps = [1, 9, 18]1是低位。9大约在中间。18是高位。- 它们之间没有简单的数学关系。
一组“看起来不错”的5输入抽头选择:
taps = [2, 5, 8, 13, 19]- 同样地,这些位置在20位的寄存器中分布得相当均匀和“无规律”。

(上面是0, 1, 2的,下面是1, 9, 18的)
(到这时又出现空字节密钥了……)
均衡下来,1, 9, 18或许可以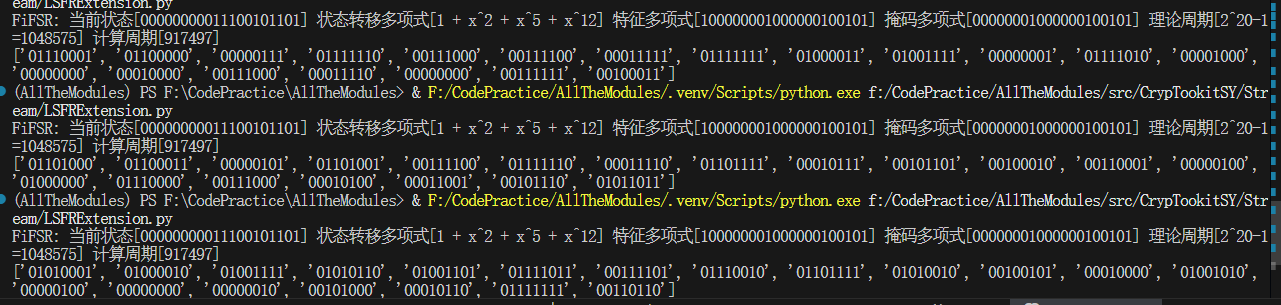
其中[1,9,18]也就是中间那行的前二十字节没有出现0x00字节段,而[2, 5, 8, 13, 19]的0/1平衡率则比[1, 9 , 18]低三个百分点
综合下来,我选择[1, 7, 17]作为进入下一个阶段前的首选
- 同样地,这些位置在20位的寄存器中分布得相当均匀和“无规律”。
FiFSR: 当前状态[00000000011100101101] 状态转移多项式[1 + x^2 + x^5 + x^12] 特征多项式[100000001000000100101] 掩码多项式[00000001000000100101] 理论周期[2^20-1=1048575] 计算周期[917497]
['01111001', '00100001', '01010111', '01111010', '00101110', '00011101', '00011111', '01111101', '01100011', '01001101', '00010010', '01001001', '00100001', '01000000', '00111000', '00001001', '00011010', '00001101', '00111111', '01011010']流密码:现代攻击手段
相关性攻击 (略)
快速相关性攻击
量子算法加持的快速相关性攻击
多采样相关性攻击
※流密码:前沿攻击技术
观测者攻击(放一下AI的回答)
論文核心思想:為“黑盒子”安裝一個“透明的監視器”
想像一下,一個流密碼生成器就像一個不透明的、內部結構複雜的“黑盒子”(這就是論文中的非線性動力系統)。您只能看到它每秒鐘吐出的一個0或1(輸出序列 z(k)),但完全不知道盒子內部成千上萬個齒輪(內部狀態 x(k))是如何轉動的。您的目標是通過觀察輸出,反推出盒子內部所有齒輪的當前確切位置。
傳統的攻擊方法(如代數攻擊)是嘗試寫出描述這個黑盒子內部所有齒輪關係的、極其複雜的非線性方程組,然後去求解,這個過程通常是NP難題,計算量極大。
而這篇論文提出的“觀測器攻擊”則另闢蹊徑,它的核心思想是:
我們能否在旁邊建造一個結構簡單、完全透明的“線性”盒子(也就是“觀測器”),讓這個透明盒子也接收黑盒子的輸出信號作為“參考”。通過不斷比較參考信號和自己內部的狀態,這個透明盒子可以在有限的時間內,將自己的狀態調整得和那個黑盒子內部的狀態完全同步。一旦同步完成,我們只需要讀取這個透明盒子的狀態,就等於知道了黑盒子的內部秘密。
這個方法之所以強大,是因為我們所有的計算都是在那個簡單的、線性的“透明盒子”裡進行的,完全繞開了直接求解複雜非線性方程的困難。
演算法的關鍵步驟與數學工具
為了實現上述思想,論文引入了幾個關鍵的數學工具和步驟:
1. 核心工具:庫普曼算子 (Koopman Operator)
這是整個演算法的理論基石。庫普曼算子的“魔力”在於,它可以將一個非線性的動力系統(狀態的演化很複雜),提升到一個更高維度的函數空間中,使其變為一個線性的動力系統。
原始系統(非線性):
x(k+1) = F(x(k)),這裡的F是一個複雜的非線性函數。提升後的系統(線性):
h(k+1) = K * h(k),這裡的h是關於原始狀態x的某個函數(稱為“可觀測量”),而K(庫普曼算子)是一個線性的矩陣。
這個過程就像是,我們不再直接觀察一個做著複雜布朗運動的粒子 x,而是去觀察這個粒子能量、動量等物理量的函數 h。雖然粒子本身的運動軌跡難以描述,但這些物理量之間的演化關係可能是簡單線性的。
2. 降維:RO-KLS (降階庫普曼線性系統)
直接使用庫普曼算子會產生一個無限維的線性系統,無法計算。因此,論文的關鍵貢獻是構建一個降階庫普曼線性系統 (Reduced Order Koopman Linear System, RO-KLS)。
目的: 找到一個維度盡可能小,但又包含了所有必要資訊(即所有內部狀態和輸出)的線性子空間。
方法: 演算法1 (Algorithm 1) 詳細描述了如何從LFSR的基礎狀態(座標函數)和非線性輸出函數
g出發,通過不斷應用庫普曼算子來擴展,直到找到一個封閉的、最小的線性空間W₁。結果: 我們得到了一個有限維度的、線性的系統,這個系統雖然比原始的LFSR複雜(例如,一個80位的LFSR,其RO-KLS可能有3240維),但它完全是線性的,可以用我們熟悉的矩陣和線性代數工具來處理。
3. 核心實現:動態觀測器 (Dynamic Observer)
有了RO-KLS這個“透明的線性模型”後,就可以建造我們的“監視器”了。這個觀測器本身也是一個動力系統,如圖4所示。
觀測器公式:
ŷ(k+1) = K₁ŷ(k) + L(z(k) - y_op(k))✰(k) = Cŷ(k)
工作流程:
ŷ(k)是觀測器猜測的內部狀態。y_op(k)是觀測器根據自己的猜測,計算出的預測輸出。z(k)是從真正的流密碼生成器那裡實際觀測到的輸出。(z(k) - y_op(k))就是“預測與現實的差距”。L是一個精心計算出的“修正增益矩陣 (observer gain)”。觀測器根據這個“差距”,通過
L來修正自己下一時刻的狀態ŷ(k+1)。只要系統是可觀測的,這個修正過程就能保證觀測器的狀態
ŷ(k)最終會收斂到RO-KLS的真實狀態y(k)。一旦
ŷ(k)收斂,我們就可以通過一個簡單的線性變換✰(k) = Cŷ(k),直接計算出原始LFSR的內部狀態x(k)。
論文中的80位LFSR攻擊實例
論文用一個非常具體的例子展示了該攻擊的可行性:
目標: 一個80位的LFSR,其輸出由3個內部狀態位的非線性函數(多数决函数)決定。
構建RO-KLS: 演算法計算出,這個80位非線性系統對應的RO-KLS是一個3240維的線性系統。
構建觀測器: 針對這個3240維的線性系統建立動態觀測器。
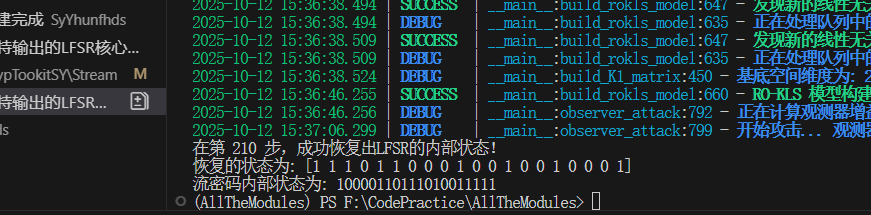
攻擊結果: 如圖5所示,觀測器在啟動後,其估計狀態與真實狀態之間的誤差(漢明距離)一開始是隨機的,但在3240步(等於RO-KLS的維度)之後,誤差驟降為0並保持。
結論: 這意味著在3240個輸出位元之後,攻擊者就完全恢復了LFSR的內部80位狀態。對於一個80位的系統來說,這是一個極其高效的攻擊。
總結
“觀測器攻擊”是一種非常新穎且強大的分析技術。它巧妙地繞過了傳統攻擊方法面對的非線性計算壁壘,其核心脈絡是:
線性化 (Linearization): 利用庫普曼算子將複雜的非線性流密碼模型,轉換為一個(通常維度更高但)完全線性的RO-KLS模型。
狀態估計 (State Estimation): 針對這個線性的RO-KLS模型,設計一個動態觀測器。
收斂與恢復 (Convergence & Recovery): 觀測器通過不斷比較真實輸出和自身預測,在多項式時間內使其內部狀態收斂,從而完全恢復出原始非線性系統的內部狀態。
這個方法將控制理論的工具成功地引入了密碼分析領域,為破解一類基於LFSR的非線性流密碼提供了全新的、在計算上可行的途徑。
※观测者攻击
何为库普曼算子
库普曼算子是一种用于描述整体属性如何随时间线性演化的规则
池塘中的每一滴水(称之为
但
- 池塘的平均温度
- 池塘水面的平均高度
- 池塘中藻类的总数量
这些整体属性是可观测的,称为可观测量(Observables),表示为
庫普曼算子的魅力在於: - 雖然單個水滴
x的運動是混亂且非線性的,但這些整體屬性g(x)的演化,在數學上卻可能是簡單且線性的。
例如,池塘的平均溫度可能只是簡單地以每小時下降0.1度的速度線性變化。

而根据论文所述,线性FSR和非线性FSR的状态更新图谱便可视为有限域上的非线性动力学系统
- 原始的非线性系统
系统的状态演化由一个非线性函数
论文中的原始公式如下: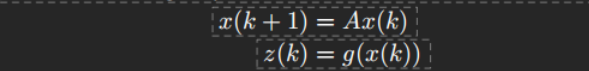
其中 - 引入可观测量
我們不再直接看x,而是選擇一個或多個關於x的函數h(x)來觀察。在論文中,這個h(x)屬於一個巨大的函數空間V⁰。
- 定义库普曼算子
庫普曼算子K的作用就是告訴我們,當系統狀態從x(k)演化到x(k+1)時,我們的觀測函數h的值會如何變化。h應用庫普曼算子,就等於計算“下一時刻”的觀測值。 - 线性化
库普曼算子本身是一种线性算子,意味着:
在数学、统计学和密码学中库普曼算子有何作用
论文的核心攻击目标,是一种被称为非线性滤波器生成器 (Non-linear Filter Generator) 的流密码(如论文图1所示)。它的结构是:
1. 一个底层的LFSR负责状态的线性更新:x(k+1) = Ax(k)。
2. 一个非线性的布尔函数 g(x) 负责从LFSR的内部状态中“采样”并组合,以生成最终的输出位:z(k) = g(x(k))。
- 核心挑战: 这种结构非常经典。由于
g(x)的非线性,我们无法再用简单的BM算法直接从输出z(k)反推出LFSR的结构。攻击者面对的是一个看似坚不可摧的“黑盒子”。
而库普曼算子是解决上述问题的根本数学原理。它就像一把能“化繁为简”的魔法棒。
- 核心功能: 它的魔力在于,能够将一个非线性的、难以分析的系统(
x(k+1) = F(x(k))),通过“升维”到一个函数空间,将其等价地转换为一个线性的、可以用矩阵解决的系统(h(k+1) = K * h(k))。 - 作用: 它为攻击者提供了一条绕过“非线性”这堵高墙的理论路径。它告诉我们:“虽然原始系统很复杂,但总存在一个与之等价的、更高维度的线性系统。”
第零步:建立一个FSR
【构建RO-KLS模型】向量化 represent_as_vector
简单来说,向量化是将抽象的数学世界翻译成计算机能够高效处理的语言的唯一桥梁。
在我们的攻击场景中,我们处理的是“函数”,例如坐标函数 χᵢ(x) 和非线性输出函数 g(x)。这些都是符号化的、抽象的数学概念。然而,我们想使用的强大武器——scipy.linalg——是一个处理具体数字(矩阵和向量)的工具。它完全不认识 x₁ 或 x₁x₅ 是什么
而向量化给了每一个抽象的单项式函数(如 x₁, x₂, x₁x₅)一个具体的、独一无二的数字身份——一个向量。
x₁不再是符号,它变成了[0, 1, 0, 0, ...]。x₁x₅不再是符号,它变成了[0, 0, 0, ..., 1, 0, ...]。 这使得我们可以在计算机中存储、比较和操作这些“函数”。
一旦所有的函数都变成了向量,整个问题就从一个复杂的“符号代数”问题,降维成了一个我们非常擅长解决的**“线性代数”**问题。- 判断线性相关性? -> 检查一个向量是否在其他向量张成的空间内,这等价于计算矩阵的秩 (Rank)。
scipy.linalg对此有高效的实现。 - 应用库普曼算子
F*? ->F*这个作用于函数上的抽象算子,现在可以被具体地表示为一个状态转移矩阵K₁。F*h的计算就变成了简单的矩阵-向量乘法。 - 求解内部状态? -> 最终,整个攻击过程变成了求解一个巨大的线性方程组,这同样可以用
scipy.linalg.solve等函数高效完成。
def create_non_linear_polynomial_universe(n: list, degree: int):
"""
对于使用degree次数非线性输出函数的n位LSFR, 穷举函数的矩阵空间\n
遍历所有可能的位元组合(每个组合都是与运算), 位元的异或和则由矩阵空间中的组合
的和表示\n
位元的下标在这里视为从1开始
你可能会觉得这操作有点像求笛卡尔积, 嗯, 对于degree=2的情形,确实像笛卡尔积运算\n
这样的话N便是可选的元素个数, degree决定<x, y, ...>关系中的元素个数;\n
但是GF2域的话不会考虑重复元素, 所以关系中的右值可以为空, 甚至空关系也包括在内\n
本函数实际使用collections.combinations生成所有组合
参数:
n: LSFR的位数
degree: 输出函数的次数; 次数为输出函数中最臃肿乘积项所包含的变量的个数
"""
universe_map = defaultdict(tuple)
index = 0 # 将位元与运算组合一一映射到自然数(包括0)上
for d in range(degree + 1):
# 从 n 个变量 (1 to n) 中,取出 d 个进行组合
for nomial_tuple in combinations(range(1, n + 1), d):
universe_map[nomial_tuple] = index
index += 1
return dict(universe_map)
def vectorize_to_n_elem_number(
n: int, d: int,
func_reprensentation_in_tuple: list[tuple],
universe_map: dict = None) -> np.ndarray:
"""
将一个函数(表示list[tuple])转换为其N元数(向量)表示\n
补充:
N元数在这里指多项式矩阵的坐标, 我怕和解析几何的坐标的弄混, 所以就改叫N元数了
Args:
func_reprensentation_in_tuple (list[tuple]): 以元组表示的g(x)函数
universe_map (dict): 函数空间映射地图
Returns:
np.ndarray: _description_
"""
if not universe_map:
cachepath = polynomials_map_cachepath
cachepath = cachepath.format(
lfsr_length=n,
poly_degree=d
)
absoulte_cachepath = cache_dir / cachepath
universe_map: dict = load_msgpack_cache(absoulte_cachepath)
universe_size = len(universe_map) # 获取其中键值对的数量
n_elem_number = np.zeros(universe_size, dtype=int) # 创建单行全零数组
for monomial_tuple in func_reprensentation_in_tuple:
# 对元组进行排序,确保与universe_map中的键匹配
sorted_monoimal_tuple = tuple(sorted(monomial_tuple))
index = universe_map.get(sorted_monoimal_tuple, None)
if index is not None: # 以防忽略index=0,也就是空元组的情况
# 异或操作
n_elem_number[index] ^= 1
"""
在密码学中这个数组将用作域(这里是GF2域)上的向量表示, 每个位置表示一个单项式组合
值为1表示该项在多项式中存在, 值为0则不存在
universe_map中的tuple: int在这里便是用于匹配单项式组合的向量的
这里不是赋值为1,而是进行模2加法,是为了避免多项式化简时可能出现的重复项问题
重复项异或自己为0, 约等于不存在, 所以采取模2加法进行模拟
"""
return n_elem_number函数空间大小为:
msgpack 在这里只是打杂缓存数据的
※【构建RO-KLS模型】 库普曼算子应用 apply_koopman
这个函数的任务,是模拟库普曼算子 F* 的作用,即进行一次符号计算,来回答这样一个问题:“当LFSR的状态从 x 演化到 F(x) 时,我们正在观察的函数 h(x) 会变成什么样的新函数?”
数学上的定义是 F*h(x) = h(F(x))
- 例如: 函数
[(1, 3), (2, 3)]。i个元素Fᵢ定义了下一时刻状态位xᵢ'的表达式。Fᵢ本身也用单项式元组列表的形式表示: - 例如: 对于一个3位的斐波那契LFSR,其更新规则是:
- 我们可以将其表示为
F = [[(2,)], [(3,)], [(1,), (2,)]]。
apply_koopman(h, F) 的核心就是模拟将 F 代入 h 的过程。这可以分解为三步:
- 符号代入
这是h(F(x))的直接翻译。我们需要遍历h的每一个单项式,并将其中每一个变量xᵢ替换成F中对应的表达式Fᵢ。- 例子: 假设
[(1, 3)])。 - 代入:
- 将
x₁替换为F₁ = [(2,)](即 - 将
x₃替换为F₃ = [(1,), (2,)](即
- 将
- 结果: 代入后我们得到一个新的表达式:
- 例子: 假设
- 展开乘积
上一步的结果通常是“和的积”的形式。我们需要用分配律将其展开成“积的和”(即代数正规范式 ANF)。在GF(2)域中,分配律是a · (b ⊕ c) = (a · b) ⊕ (a · c)。- 例子: 展开
- 展开:
- 结果: 得到一个函数,其单项式列表为
[(1, 2), (2, 2)]。
- 例子: 展开
- 化简
展开后的结果可能包含需要化简的项。在GF(2)域中,主要有两条化简规则:- 幂等律:
- 对合律:
- 例子: 化简
[(1, 2), (2, 2)] - 应用幂等律:
(2, 2)->(2,)
- 结果: 化简后的单项式列表为
[(1, 2), (2,)]。
如果展开后出现重复的项,例如[(1, 2), (1, 3), (1, 2)],它们会根据对合律相互抵消,最终结果是[(1, 3)]。
- 幂等律:
注
我搞到这里才发现这个攻击的目标是恢复初始密钥,而不是恢复密码结构
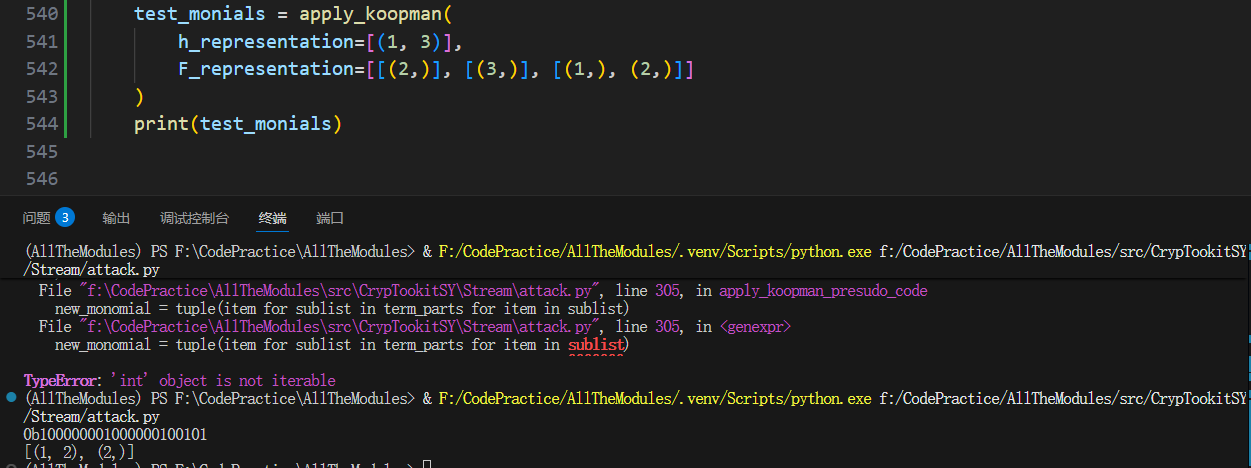
【构建RO-KLS模型】线性独立判断 is_linearly_dependent
要判断一个新向量是否可以被一组现有的基底向量线性表示,最高效、最标准的数学工具就是矩阵的秩 (Matrix Rank)。
- 秩的含义: 一个矩阵的秩,等于其内部线性无关的行(或列)向量的最大数量。通俗地说,它代表了这个矩阵所包含的向量能够“张成”的空间维度。
- 我们的判断逻辑:
- 我们将现有的基底向量
B组成一个矩阵M,并计算它的秩rank(M)。 - 我们将新向量
v添加到基底中,形成一个更大的矩阵M',并计算它的秩rank(M')。 - 比较两个秩:
- 如果
rank(M') == rank(M),说明新向量v没有为这个空间增加任何新的维度。它完全“躺”在旧基底张成的空间内,因此它是线性相关的。 - 如果
rank(M') > rank(M),说明新向量v指向了一个全新的方向,它无法被旧基底表示。因此,它是线性无关的。
- 如果
- 我们将现有的基底向量
def is_linear_dependent(
new_vector: np.ndarray,
basis: list[np.ndarray]
) -> bool:
"""
使用矩阵的秩来判断一个新向量是否与一个基底(向量列表)线性相关。
:param new_vector: 需要被判断的“N元数”向量。
:param basis: 当前已有的“N元数”基底列表。
:return: 如果线性相关,返回 True;如果线性无关,返回 False。
"""
if not basis:
return not np.any(new_vector)
"""
如果basis基底矩阵为空, 那么任何非零向量都是线性无关的
"""
basis_matrix = np.array(basis, dtype=int)
"""
构建基底矩阵; 标准的实现需要考虑浮点数, 但鉴于这里是GF(2)域, 域中只有0和1,
所以可以不考虑浮点数
"""
rank_old = nlinalg.matrix_rank(basis_matrix) # 计算基底的秩
extended_matrix = np.vstack([basis_matrix, new_vector]) # 构建扩展矩阵, 把新的向量添加为新的一行
rank_new = nlinalg.matrix_rank(extended_matrix) # 计算扩展矩阵的秩
return rank_old == rank_new # 如果基底矩阵的秩有变, 那么新的向量是线性无关的->这说明维度得到了拓展【构建RO-KLS模型】线性系统矩阵构建 build_linear_system_matrices
目标是计算出三个核心矩阵:K1, C, 和 Gamma,它们共同定义了一个标准线性时不变(LTI)系统:
- 状态演化方程:
- 观测方程:
- 状态重构方程:
y(k)则是RO-KLS在k时刻的状态向量。我们的任务就是计算出K₁、C和Γ这三张“规则图”。
- 矩阵
K₁:状态转移矩阵 (State Transition Matrix)- 它的作用是什么?
K₁是RO-KLS这个线性系统的“引擎”或“状态更新规则”。它描述了如果您知道当前时刻k的高维状态向量y(k),如何计算出下一时刻k+1的状态y(k+1)。它等价于原始非线性系统中F(x)的作用,但却是完全线性的。 - 如何构建它?
K₁将是一个D x D的方阵(D是您基底的大小)。构建它的方法非常直接:K₁的第j列,就是对基底中第j个函数ψⱼ应用库普曼算子F*后的结果的“N元数”表示。
- 它的作用是什么?
- 矩阵
C:状态恢复矩阵 (State Recovery Matrix)- 它的作用是什么?
C是一个“解码器”。它的作用是将RO-KLS的高维状态向量y(k),解码回我们真正关心的、原始的、低维的LFSR内部状态x(k)。 - 如何构建它?
C将是一个n x D的矩阵(n是原始LFSR的位数)。构建它也非常简单:C的第i行,就是坐标函数χᵢ(即xᵢ) 的“N元数”表示。
- 它的作用是什么?
- 矩阵
Γ(Gamma):输出矩阵 (Output Matrix)
- 它的作用是什么?
Γ是一个“观测器”的探头。它描述了如何从RO-KLS的高维状态向量y(k)中,计算出我们唯一能从外部看到的那个单比特输出z(k)。 - 如何构建它?
Γ将是一个1 x D的矩阵(即一个行向量)。它的构建最为直接:Γ就是您的非线性输出函数g(x)的“N元数”表示。
第一步:构建RO-KLS(降阶库普曼)模型
这块太恐怖了……性能开销和计算都很头大
构建坐标函数
补习基础
在数学中,当我们有一个多维空间(比如一个n维非线性向量空间 x,它可以写成一个包含n个比特的向量:
坐标函数 (Coordinate Function),在论文中用希腊字母 x 进行的最基本、最简单的“测量”。第 i 个坐标函数 x 中,把第 i 个分量 xᵢ “挑”出来。
坐标函数的通用公式 ,便是论文中给出的那个极其简洁的定义:
让我们把它放在熟悉的编程情境中来理解:
x就像一个数组或列表,例如state = [1, 0, 1, 1]。- 坐标函数
χ₃就相当于一个Python函数lambda state: state[2](使用0-based索引)。
所以,坐标函数不是什么复杂的东西,它就是一次最简单的“取值”或“投影”操作。
既然坐标函数如此简单,为什么它在这篇论文中如此重要呢?
因为它们是构建整个高维线性世界(RO-KLS)的**“原子”或“基本积木”** 。观测器攻击的最终目标,就是恢复出LFSR在某一时刻的完整内部状态 (x₁, x₂, ..., xₙ)。这意味着,我们的线性模型必须包含能够代表 x₁ 到 xₙ 这些值的信息。坐标函数 χᵢ 正是这些信息的直接载体。
论文中的构建流程 (Algorithm 1) 正是基于这个思想 :
- 确定“种子”函数: 攻击者将所有的坐标函数
χ₁, ..., χₙ和非线性输出函数g(x)一起,作为构建线性空间的“种子”集合。 - “衍生”新函数: 攻击者开始对这些“种子”函数反复应用库普曼算子
F*(即LFSR的下一状态逻辑)。F*(χᵢ)会得到一个新的函数,这个函数描述了“下一时刻LFSR第i位的值是多少”。F*²(χᵢ)则描述了“下下时刻...”。
- 构建“封闭”空间: 这个“衍生”过程会不断产生新的、更复杂的函数(通常是更高次的单项式,如
xᵢxⱼ)。直到我们发现,所有新衍生的函数都已经可以被现有函数集合的线性组合(异或和)所表示时,这个过程就结束了。
最终得到的这个“封闭”的函数集合,就是RO-KLS的基底 (Basis) 。它就像一个高维空间的坐标系,而χ₁到χₙ则是这个坐标系中最基础的几个坐标轴。
注意事项
误区:坐标函数就是状态
- 需要区分
χᵢ和xᵢ。xᵢ是一个值(0或1),而χᵢ是一个函数,这个函数的作用是返回xᵢ的值。在库普曼算子的世界里,我们操作的对象是函数本身,而不是数值。
- 需要区分
注意事项:它们是攻击的起点和终点
坐标函数是构建RO-KLS的起点,因为它们代表了我们想要恢复的基础信息。
最终,当观测器成功恢复出RO-KLS的高维状态向量
y(k)后,我们通过一个简单的矩阵乘法x(k) = Cy(k),就能从这个高维向量中“解码”出χ₁到χₙ在那一时刻的值,从而恢复出完整的LFSR状态。
第二步:观测器攻击
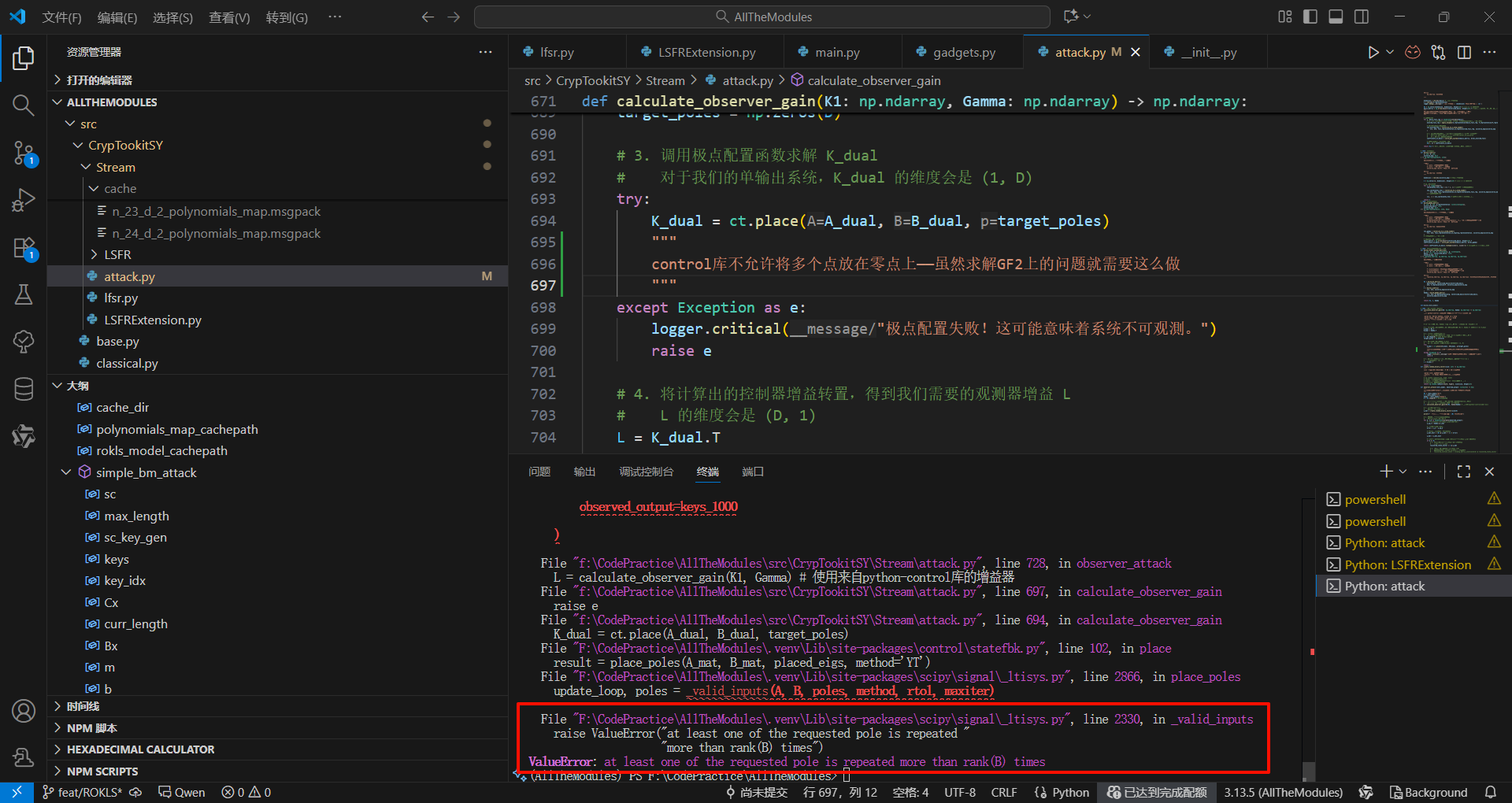
不给我把多个点放在极点上……
Gemini神力
【观测器攻击】GF2域上的矩阵乘法
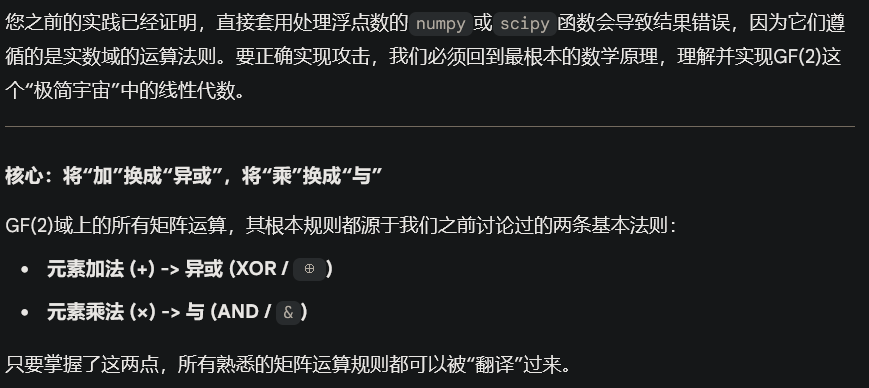
(已经放弃了,晕了)
完全是AI在写了
【观测器攻击】GF2上的极点配置算法
control库的东西是针对浮点数的,对于GF2域来说有点超纲了……
control.place 這類為通用浮點數系統設計的工具,無法處理我們的特殊需求:將所有極點(特徵值)都放在0上(这样
這個演算法就是阿克曼公式 (Ackermann's formula)。
在深入算法之前,我们必须再次明确我们的目标。
- 我们有一个线性系统,其误差的演化由矩阵
A_e = K₁ - LΓ决定。 - 我们希望这个误差能尽可能快地衰减到零。
- 在一个D维的离散系统中,“最快”的收敛意味着,在最多D步之后,误差必须为零。
- 能实现这一点的矩阵,被称为幂零矩阵 (Nilpotent Matrix),即存在一个整数
d <= D,使得 (Ae)d=0。 - 一个矩阵是幂零的,其充要条件是它的所有特征值 (Eigenvalues) 都等于0。
所以,我们的核心任务就变成了:
找到一个增益向量
L,使得矩阵K₁ - LΓ的所有D个特征值(“极点”)都被精确地“配置”在复平面的原点0上。
对于我们这种情况——一个单输入系统(因为 Γ 只有一行,所以 Γ.T 只有一列),阿克曼公式提供了一个直接计算增益矩阵 L(在对偶问题中是K_dual)的“配方”。
数学原理: 该公式基于一个深刻的线性代数定理——凯莱-哈密顿定理 (Cayley-Hamilton Theorem),该定理指出任何一个方阵都满足其自身的特征方程。阿克曼公式巧妙地利用这个定理,通过一系列矩阵运算,直接构造出我们想要的增益向量。
公式 (对偶版本): 给定一个对偶系统 (A_d, B_d)(在我们的代码中是 A_dual=K₁.T, B_dual=Γ.T),要将系统的极点配置到目标特征多项式 α(s) 所定义的位置,其控制器增益 K_dual 可以这样计算:
花絮
搜集资料
(抱歉长官,刚刚没认出来是你)
了解观察者攻击的可行性
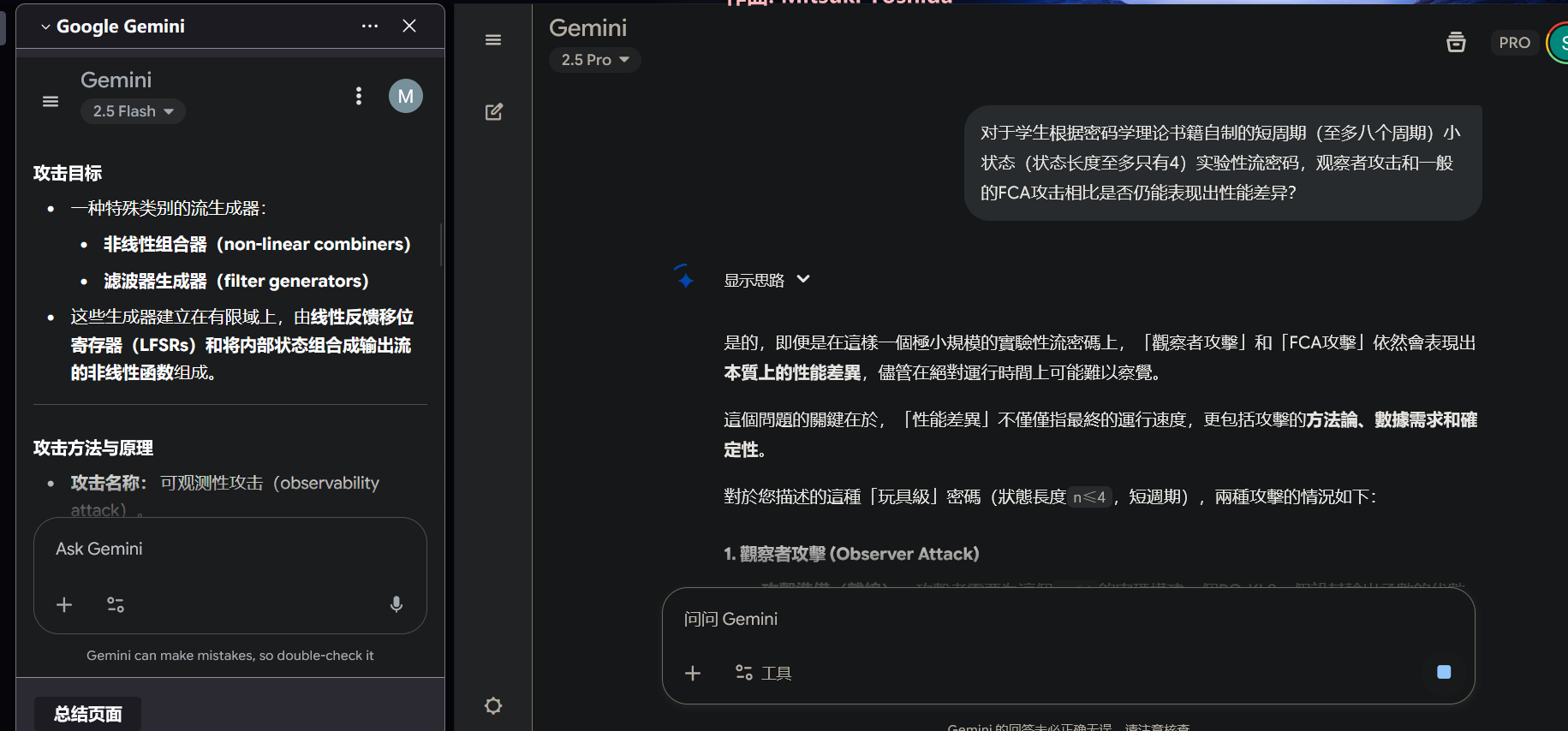
看起来应该没问题,就这个了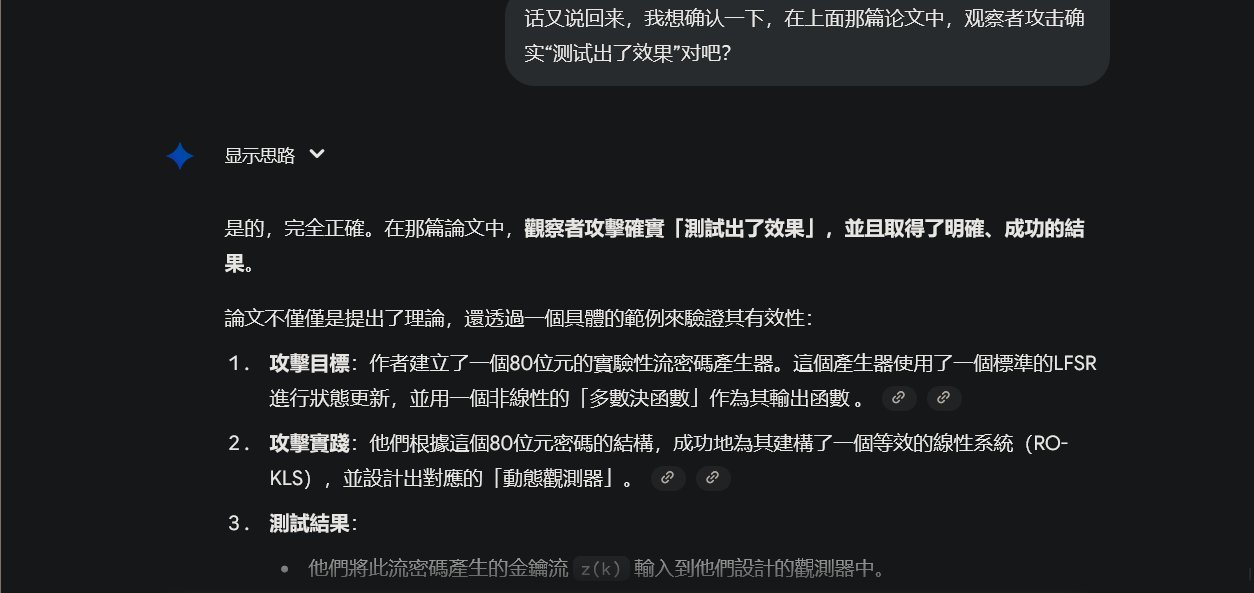

理论可行,那么……?
写代码
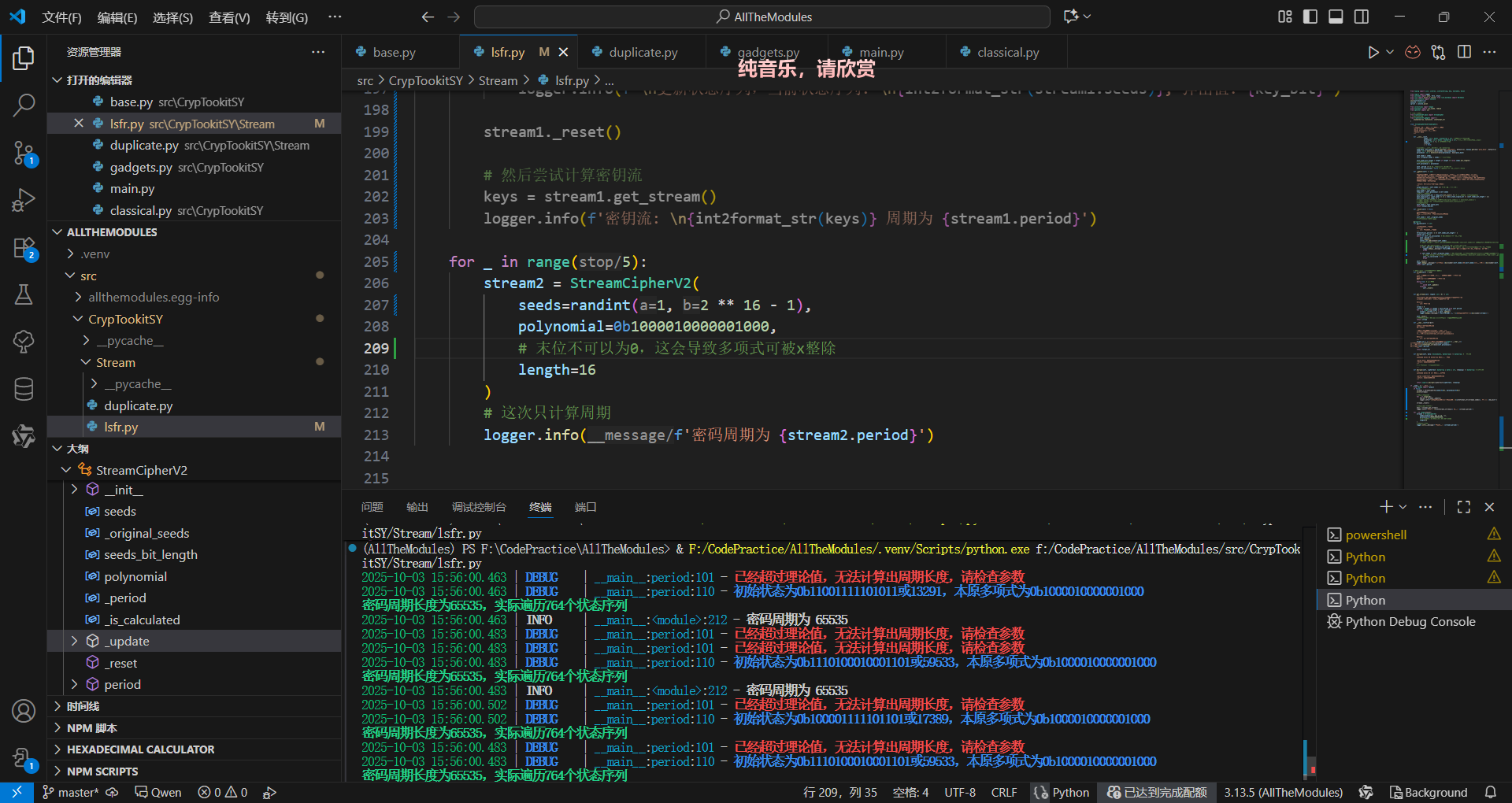
stream2 = StreamCipherV2(
seeds=randint(1, 2 ** 16 - 1),
polynomial=0b1000010000001000,
# 末位不可以为0,这会导致多项式可被x整除
length=16
)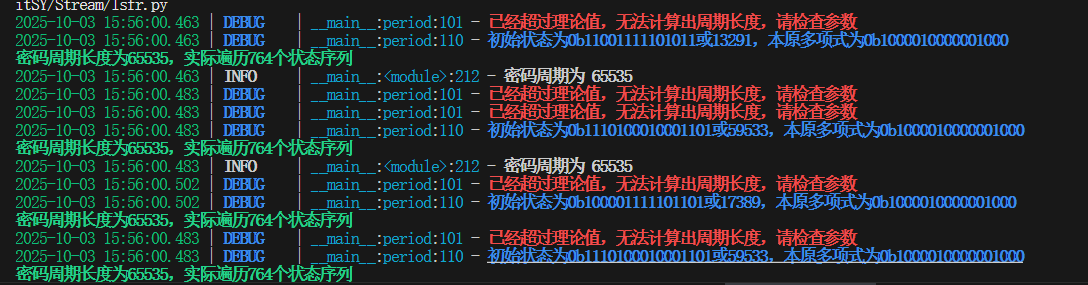
多项式最后一位为0导致循环状态不连续
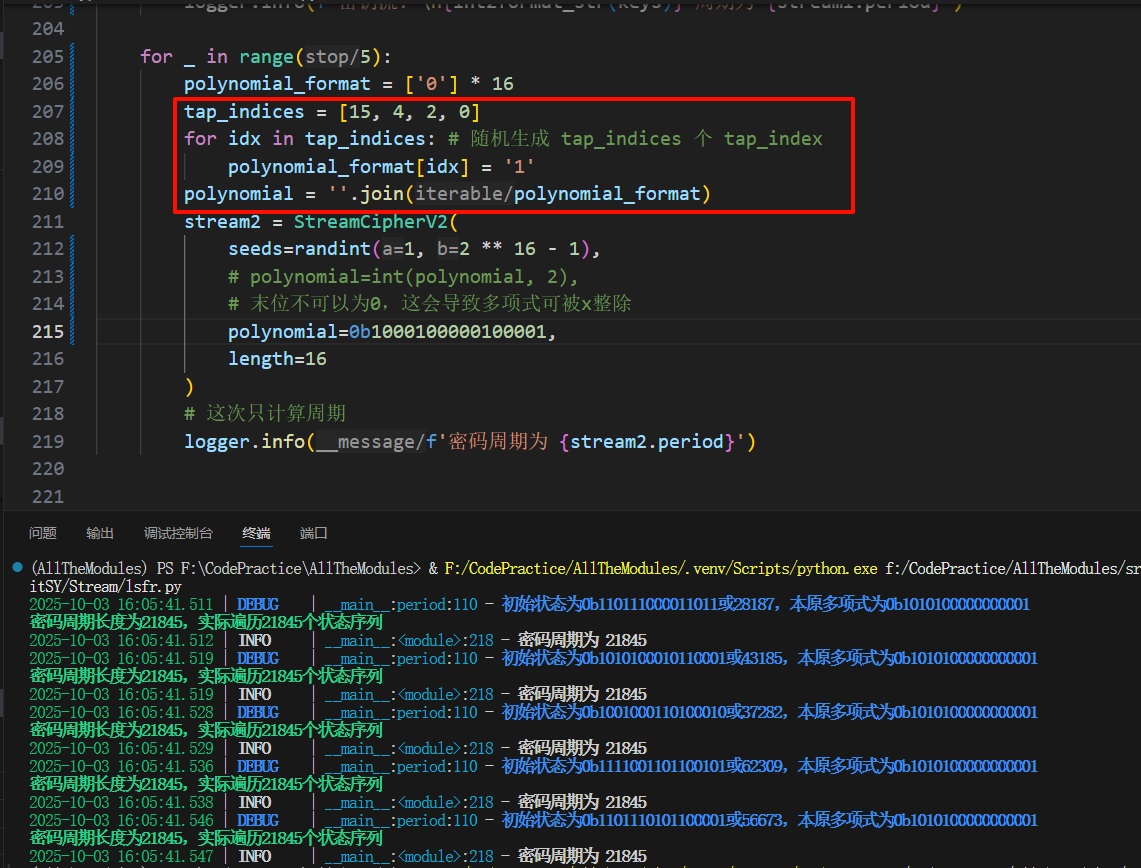

手动生成抽头序列后产生了不可约的多项式
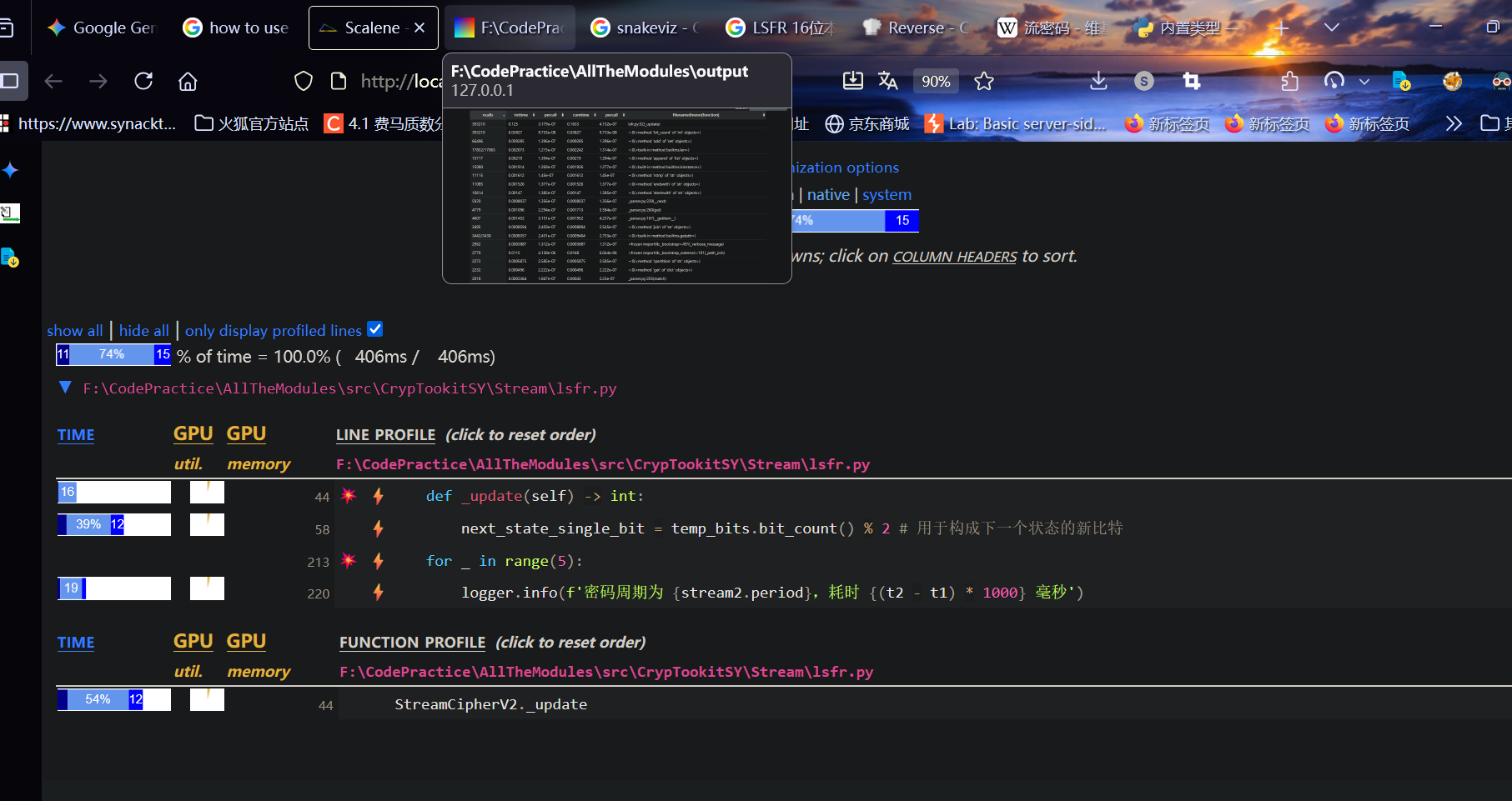
woc了怎么优化完还能更慢
寄吧了这函数开销……
试图改成列表推导式,然后被字符串长度限制斩于马下
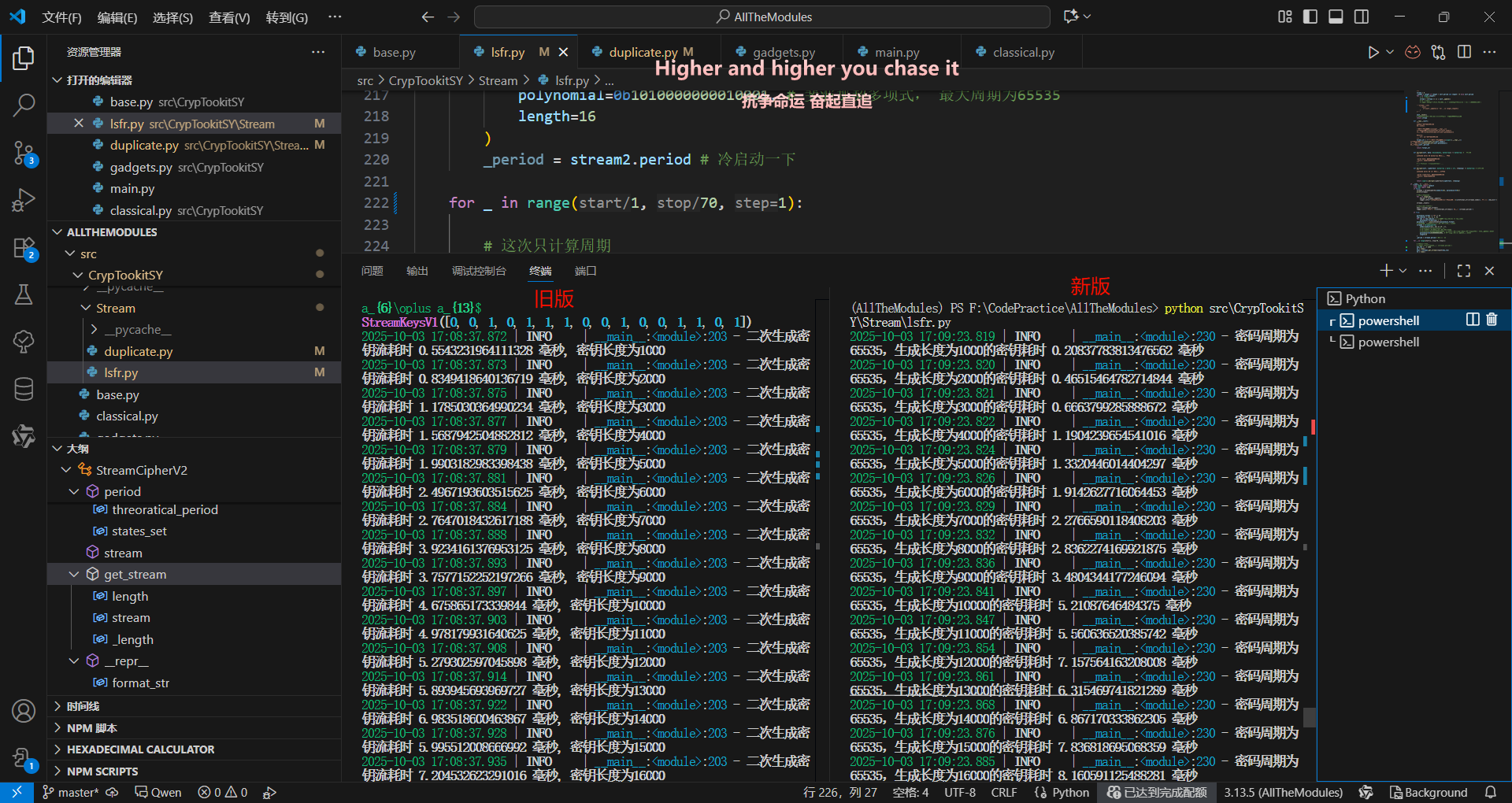
左边的耗时是线性增长,右边是指数增长……
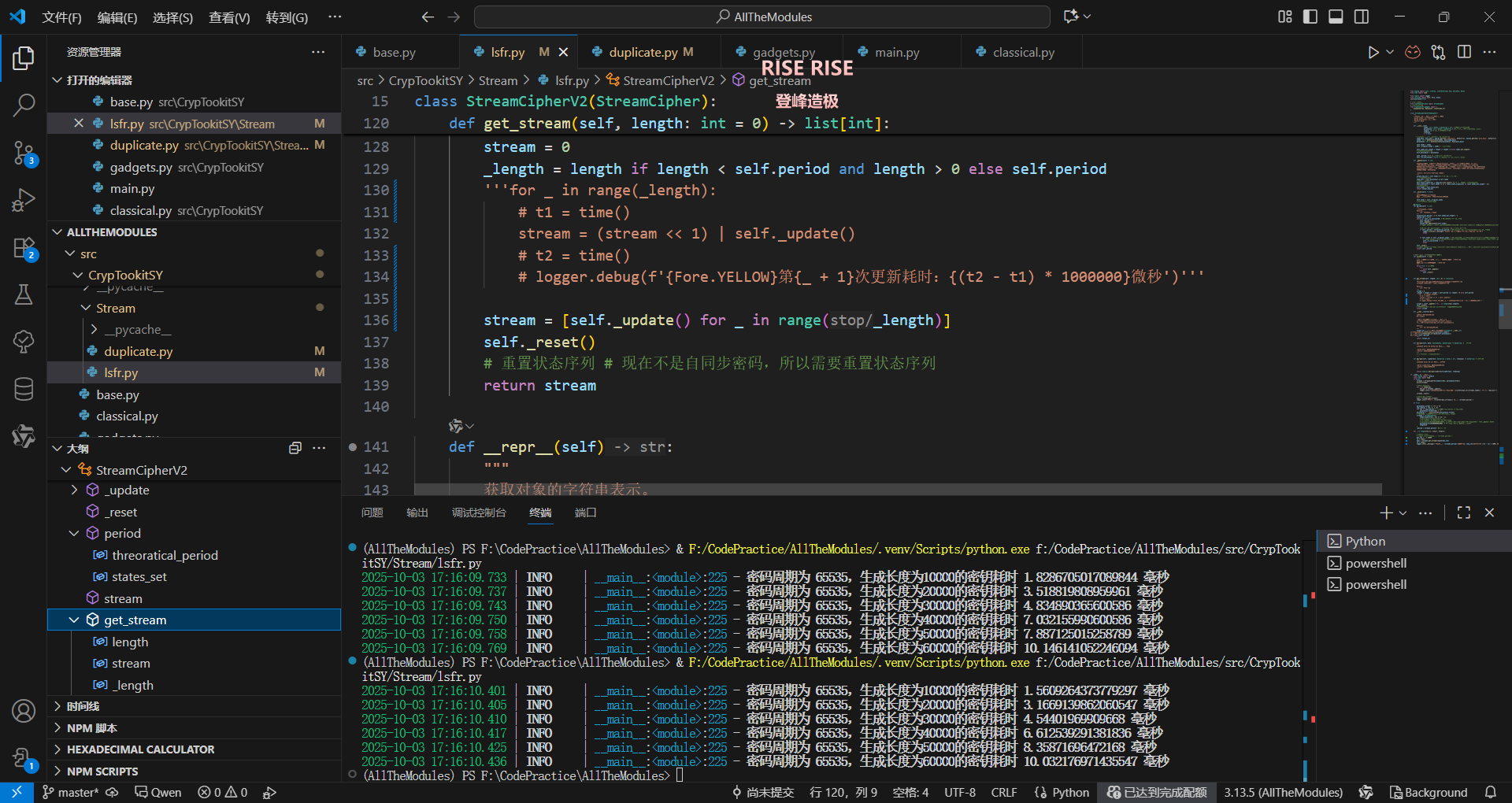
换成列表推导式之后速度提升2.5倍平均
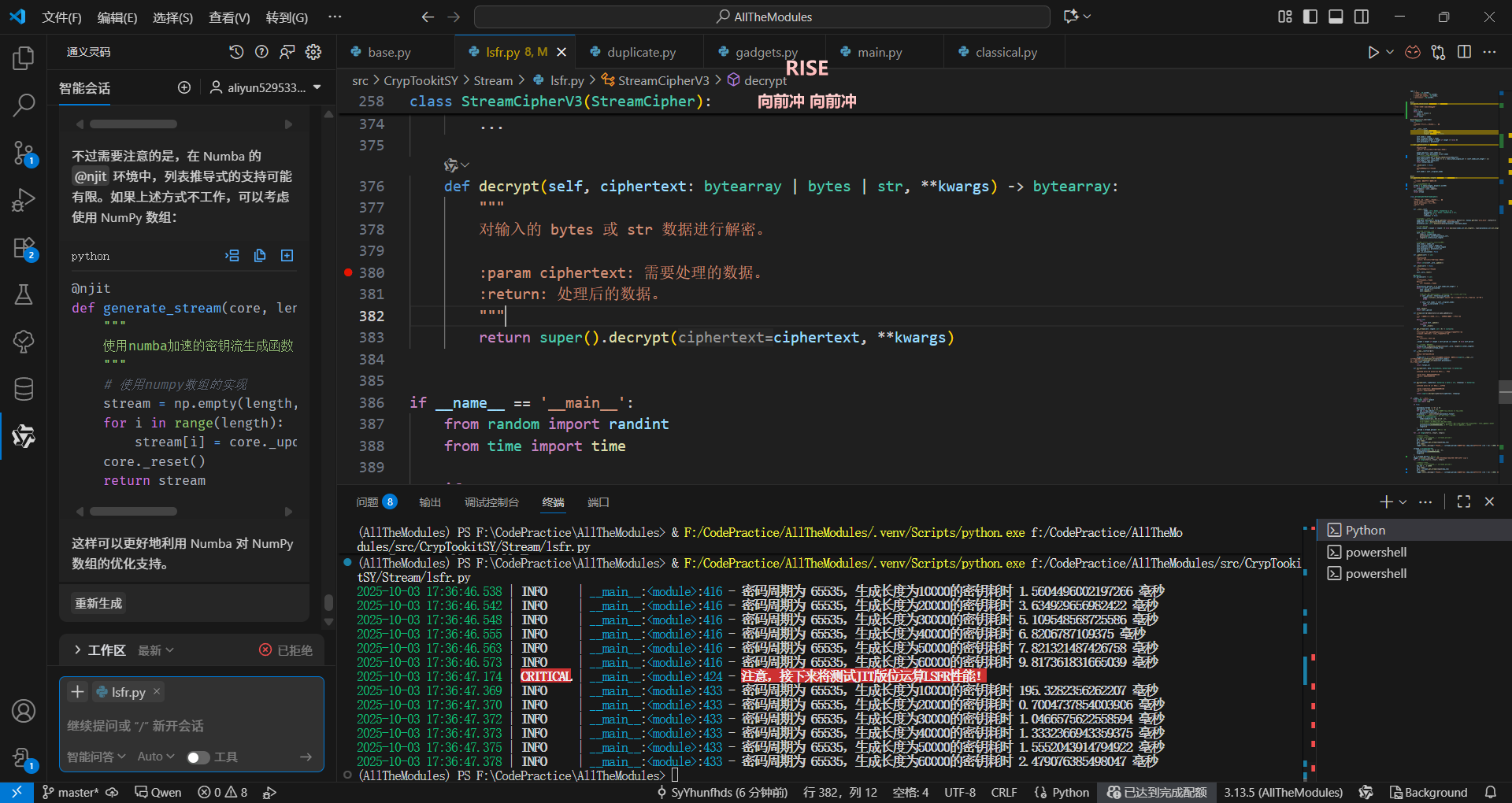
AI助力JIT应用
不过这第一次有点爆炸,可能是因为JIT编译不是事先编译好的
(其实JIT这部分是AI写的)
漫长重构

能用就行
现在已经彻底乱套了


拨乱反正
第三代
超长多项式加超短初始状态的后果——密钥空转

没有预热的后果……
向量化
AI才能救了