观测器攻击
2025/10/12大约 8 分钟
文献来源
参考资料
热身准备
构建LFSR(线性反馈移位寄存器)
根据维基百科所述,基础的LFSR线性反馈移位寄存器分为斐波那契LFSR和伽罗瓦LFSR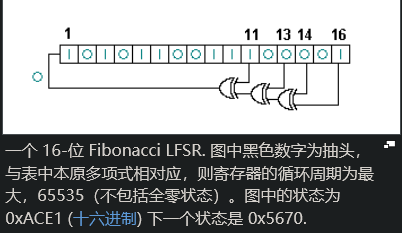
在LFSR中,抽头的设定可以用有限域算数中模2的多项式来表示。这就意味着,多项式中的所有系数必须是“1”或者“0”。这个多项式被称作回授多项式或特征多项式。例如图中的抽头为在第16,14,13,11个比特,则相应的特征多项式为:
斐波那契LFSR和伽罗瓦LFSR均使用抽头序列控制参与反馈运算的比特位,二者也都会提取寄存器末尾(图上是
伽罗瓦LFSR是否进行反馈运算取决于抽出的比特是
在计算新的状态前,两种LFSR寄存器中的值都会后移一位——然后,斐波那契LFSR会将反馈位置于寄存器最前面,而伽罗瓦LFSR直接将寄存器空出来的一位视为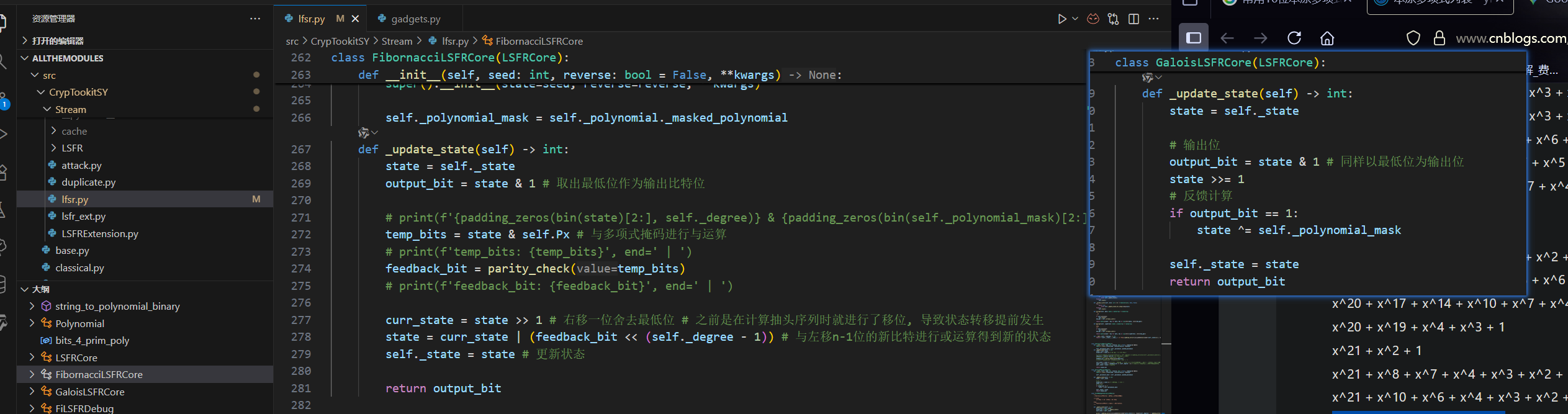
代码测试结果如下:
FibornacciLSFRCore: 当前状态[000000000000000000001] 状态转移多项式[1 + x^2 + x^5 + x^13] 特征多项式[1000000010000000100101] 掩码多项式[000000010000000100101] 理论周期[2^21-1=2097151] 计算周期[2097151]from functools import reduce
from random import randint
from typing import Any, Generator
import re
from CrypTookitSY.base import BaseCipher, StreamCipher
from CrypTookitSY.gadgets import padding_8_zeros, parity_check, padding_zeros, reverse_polynomial
from colorama import init, Fore, Style
init(autoreset=True)
def string_to_polynomial_binary(polynomial_str: str) -> int:
"""
保持项的顺序处理的版本(虽然对于结果没有影响)
多项式字符串格式为: 1 + x + x^4 + x^5, 则会映射得到多项式整数 0b110011
Args:
polynomial_str (str): 指数形式的多项式字符串
Returns:
int: 二进制表示的多项式
"""
# 移除所有空格
clean_str = re.sub(r'\s+', '', polynomial_str)
# 找到所有项及其在字符串中的位置
term_matches = list(re.finditer(r'1|x\^\d+|x', clean_str))
# 按在字符串中出现的顺序处理项
exponents = []
for match in term_matches:
term = match.group()
if term == '1':
exponents.append(0)
elif term == 'x':
exponents.append(1)
else:
# 匹配 x^n 形式
exp_match = re.match(r'x\^(\d+)', term)
if exp_match:
exponents.append(int(exp_match.group(1)))
# 计算二进制表示
result = 0
for exp in exponents:
result |= (1 << exp)
return result
class Polynomial:
__slots__ = ('_symbol_polynomial', '_masked_polynomial', 'degree', '_mask', '_string_polynomial')
def __init__(self, polynomial: int | str, reverse: bool = False):
"""
一个用于存储和表示多项式的类
Note:
以Polynomial=0b110011为例, 映射得到的特征多项式C(x)为
$C(x) = 1 + x + x^4 + x^5$\n
其中最高项是规则项, 不参与状态转移, 应被舍去, 得到
$P(x) = x + x^4 + x^5$\n, 表示第1, 4, 5位比特参与运算, 与之对应的状态比特则分别为a_4, a_1, a_0
二进制表示形式即舍去了最高位的0b110011,或0b10011
本类的__repr__()方法会返回状态转移多项式P(x)的表示形式\n
Polynomial映射到x多项式上时, 指数是递增的——出于程序实现考量, 如果按照大端序设计映射规则,
则生成掩码多项式时是舍去最低位, 反而要求最高位必须是1, 这样会降低掩码多项式的自由度
Args:
polynomial (int | str): 多项式整数; 也可以是字符串
reverse (bool = False): 是否将多项式进行倒数反转, 目前的实现将多项式视为小端序, 但会舍弃最高位\n
若启用该选项, 则将计算特征多项式的倒数用于实际的特征多项式
"""
if isinstance(polynomial, str):
polynomial = string_to_polynomial_binary(polynomial)
self.degree = polynomial.bit_length() - 1
if reverse: # 标准化
polynomial = reverse_polynomial(polynomial, self.degree)
self._symbol_polynomial = polynomial
self._mask = (1 << self.degree) - 1
self._masked_polynomial = polynomial & self._mask
_bin_string_polynomial = bin(self._masked_polynomial)[2:][::-1]
_start_string_polynomial = '1' if _bin_string_polynomial[0] else ''
_x_string_polynomial = (
f'x^{exp+1}' if exp >= 1 else f'x'
for exp, tap_indice in enumerate(_bin_string_polynomial[1:]) if tap_indice == '1'
)
_string_nomial_seq = [_start_string_polynomial] + list(_x_string_polynomial)
self._string_polynomial = ' + '.join(_string_nomial_seq)
@property
def poly(self) -> int:
return self._symbol_polynomial
@property
def mask(self) -> int:
return self._masked_polynomial
@property
def reducible(self) -> bool:
"""
判断本原多项式是否为可约多项式, 如果最低比特也就是对应于C(x)中的1项, \n
其系数为0,则实例所存储的多项式为可约多项式
Returns:
bool: _description_
"""
return (self._symbol_polynomial & 0b1) == 0
def __repr__(self) -> str:
return self._string_polynomial
bits_4_prim_poly = Polynomial(0b11011)
class LSFRCore:
def __init__(
self,
polynomial: int, # 特征多项式(整型)
state: int | None = None, # 状态序列
autoreset: bool = True, # 加解密前是否自动重置状态序列
reverse: bool = False, # 是否将多项式序列进行标准化
randomize: bool = False, # 是否启用随机输出密钥比特
):
self._polynomial = Polynomial(polynomial=polynomial)
self._degree = self._polynomial.degree
self._state = state
self._initial_state = state
self._period = 0
self._expected_max_period = 2**self._degree - 1
self._calculated = False # 是否已经计算过周期
self._randomize = randomize
def _non_linear_output(self) -> int:
"""
非线性输出
"""
return randint(0, 1) # 这个只是占位的
def _update_state(self) -> int:
"""
更新状态序列
"""
if self._randomize:
return self._non_linear_output() # 向前兼容, 所以update_state仍然必须返回输出比特
return 1
def _update_state_for_steps(self, steps: int = 1):
if steps == 1:
output_bit = self._update_state() # 占位的
return output_bit
elif steps <= 0:
raise ValueError('用于更新状态的步长必须为正整数')
output_bits = 0
for _ in range(steps - 1):
output_bit = self._update_state() # 占位符
output_bits = output_bits << 1 | output_bit
return output_bits
def reset(self):
self._state = self._initial_state
def _calc_period(self) -> bool:
visited_rounds = 0
for _ in range(self._expected_max_period):
visited_rounds += 1
# prev_state = self._state
out = self._update_state()
# print(f'{padding_zeros(bin(prev_state)[2:], self._degree)} -> {padding_zeros(bin(self._state)[2:], self._degree)} OUT: {out}')
if self._state == self._initial_state:
self._period = visited_rounds
self.reset()
return True
self._calculated = True
self.reset()
"""
在完成了理论最大周期次数的遍历后, 如果仍然回不到初始状态, 就说明多项式存在问题
"""
return self._state == self._initial_state
@property
def Px(self) -> int:
"""
获取抽头/掩码多项式
"""
return self._polynomial._masked_polynomial
@property
def Cx(self) -> int:
"""
获取特征多项式
"""
return self._polynomial._symbol_polynomial
@property
def Fx(self) -> int:
"""
获取掩码多项式的x^n表现形式字符串
"""
return self._polynomial._string_polynomial
@property
def period(self) -> int:
if not self._calculated:
self._calc_period()
return self._period
@property
def reducible(self) -> bool:
return self._polynomial.reducible
@property
def primitive(self) -> bool:
"""
判断实例存储的多项式是否为本原多项式, \n
如果可约,且周期为2^n-1,则多项式确实为本原多项式
"""
return (not self._polynomial.reducible) and self.period == 2**self._degree - 1
def keys(self, length: int = 0) -> Generator[int, Any, None]:
"""
生成密钥流; 若length不为正整数, 则校正为理论周期值
"""
length = length if length > 0 else self._expected_max_period
try:
for _ in range(length):
yield self._update_state()
finally:
self.reset()
def _stream_n_bits(self, bits: int = 8) -> Generator[int, None, None]:
try:
while True:
yield self._update_state_for_steps(bits)
finally:
self.reset()
def encrypt(self, data: bytes | bytearray) -> bytearray:
"""
加密
"""
if self.autoreset:
self.reset()
key_gen = self._stream_n_bits()
return bytes(byte ^ key for byte, key in zip(data, key_gen))
def decrypt(self, ciphertext: bytes | bytearray) -> bytearray:
"""
解密
"""
if self.autoreset:
self.reset()
key_gen = self._stream_n_bits()
return bytes(byte ^ key for byte, key in zip(ciphertext, key_gen))
def __repr__(self, **kwargs) -> str:
return f'{self.__class__.__name__}: 当前状态[{padding_zeros(bin(self._state)[2:], self._degree)}] 状态转移多项式[{self._polynomial}] 特征多项式[{padding_zeros(bin(self.Cx)[2:], self._degree)}] 掩码多项式[{padding_zeros(bin(self.Px)[2:], self._degree)}] 理论周期[2^{self._degree}-1={self._expected_max_period}] 计算周期[{self.period}]'
class FibornacciLSFRCore(LSFRCore):
def __init__(self, seed: int, reverse: bool = False, **kwargs):
super().__init__(state=seed, reverse=reverse, **kwargs)
self._polynomial_mask = self._polynomial._masked_polynomial
def _update_state(self) -> int:
state = self._state
output_bit = state & 1 # 取出最低位作为输出比特位
# print(f'{padding_zeros(bin(state)[2:], self._degree)} & {padding_zeros(bin(self._polynomial_mask)[2:], self._degree)} -> ', end='')
temp_bits = state & self.Px # 与多项式掩码进行与运算
# print(f'temp_bits: {temp_bits}', end=' | ')
feedback_bit = parity_check(temp_bits)
# print(f'feedback_bit: {feedback_bit}', end=' | ')
curr_state = state >> 1 # 右移一位舍去最低位 # 之前是在计算抽头序列时就进行了移位, 导致状态转移提前发生
state = curr_state | (feedback_bit << (self._degree - 1)) # 与左移n-1位的新比特进行或运算得到新的状态
self._state = state # 更新状态
return output_bit
class GaloisLSFRCore(LSFRCore):
def __init__(self, seed: int, reverse: bool = False, **kwargs):
super().__init__(state=seed, reverse=reverse, **kwargs)
self._polynomial_mask = self._polynomial._masked_polynomial
def _update_state(self) -> int:
state = self._state
# 输出位
output_bit = state & 1 # 同样以最低位为输出位
state >>= 1
# 反馈计算
if output_bit == 1:
state ^= self._polynomial_mask
self._state = state
return output_bit
class FiLSFRDebug(FibornacciLSFRCore):
"""
为FibornacciLSFRCore添加了状态转移时的打印功能
格式示例:
当前状态 -> 下一个状态 | 输出比特
Args:
FibornacciLSFRCore (_type_): _description_
"""
def _update_state(self) -> int:
prev_state = self._state
output_bit = super()._update_state()
next_state = self._state
print(f'{padding_zeros(bin(prev_state)[2:], self._degree)} -> {padding_zeros(bin(next_state)[2:], self._degree)} | {Fore.GREEN}{output_bit}{Style.RESET_ALL}')
return output_bit
if __name__ == '__main__':
filsfr = FibornacciLSFRCore(seed=0b01, polynomial=0b1101, reverse=True)
print(filsfr)
filsfr = FibornacciLSFRCore(seed=0b01, polynomial="x^21 + x^13 + x^5 + x^2 + 1")
print(filsfr)
filsfr_debug = FiLSFRDebug(seed=0b101, polynomial=0b1011)
print(filsfr_debug)
# 测试各种顺序和格式
test_cases = [
"1 + x + x^4 + x^5",
"x^5 + x^4 + x + 1",
"1+x+x^4+x^5",
"x^5+x^4+x+1",
"x + 1 + x^5 + x^4"
]
for test_str in test_cases:
result = string_to_polynomial_binary(test_str)
print(f'C(x) = "{test_str}" -> Polynomial={bin(result)} (0b{bin(result)[2:]})')为LFSR加上非线性密钥输出
搭建ROKLS线性系统模型
用向量描述坐标函数
创建基底空间
矩阵运算如何描述状态转移
库普曼演化
矩阵如何统一到各式各样的基底空间中
最终线性系统搭建
正文
观测器攻击
重写GF2域上的矩阵运算
为什么原版Numpy不行?
重构矩阵运算
观测器攻击原理重申
配置多极点实现最速收敛
花絮
洋洋洒洒上百页PDF
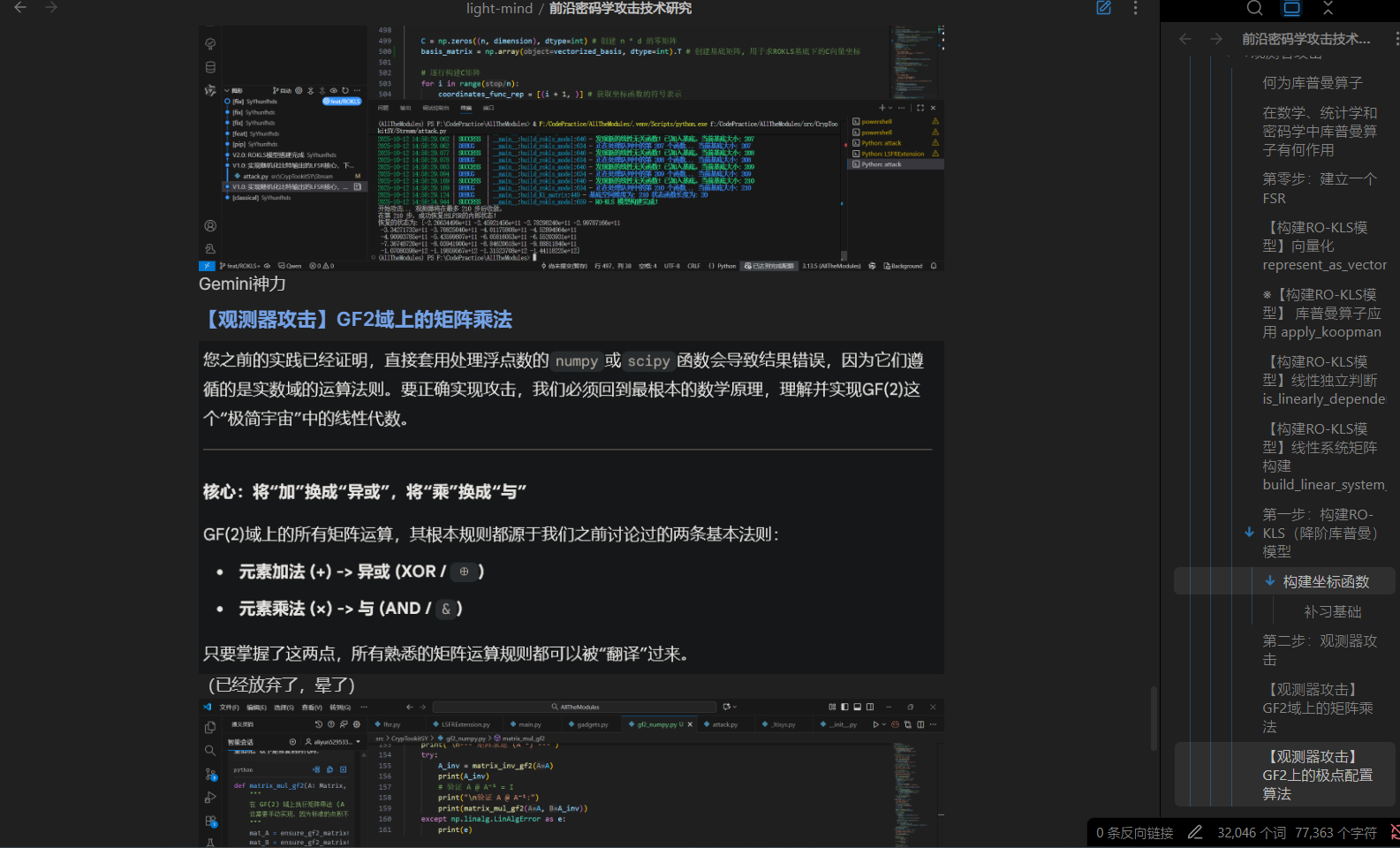
嗯,没有我自己的话